Спроможність за Смітом . Якщо множина А кандидатів розбивається на дві підмножини В ₁ , B₂ , що не перетинаються, і кожний кандидат b₁ ÎВ ₁ виграє (за суворою більшістю) у будь-якого кандидата b₂ ÎВ ₂ , то повинний бути обраний результат із В ₁ .

З іншого боку, голосування при послідовному винятку очевидно не є нейтральним. Порядок виключень, звичайно, впливає на результат.

Правило рівнобіжного виключення . Спочатку за правилом більшості дорівнюються пари а з b і с з d . Переможці зустрічаються у фіналі, де порівнюються за правилом більшості. У випадку рівності вибирається кандидат, що йде раніше за алфавітом.

Це - знову заможний за Кондорсе метод. Більш того, для обрання кожному кандидату х потрібно перемогти в двох порівняннях за правилом більшості. Припустимо спочатку, що рівності при порівнянні з цими двома кандидатами немає (х виграє для суворої більшості). Тоді х не може домінуватися за Парето деяким кандидатом у , інакше b був би переможцем за Кондорсе. Отже, метод рівнобіжного виключення вибирає оптимальний за Парето результат у (найбільше поширеному) випадку, коли при бінарних виборах немає рівностей. Проте якщо рівності можливі, то оптимальність за Парето може порушуватися.

Бінарним деревом на А є таке кінцеве дерево, у котрому кожній нефінальній вершині (включаючи початкову) відповідають рівно дві наступні, а кожній фінальній вершині (у котрої немає наступних) приписаний кандидат (елемент із A ), причому кожний кандидат з'являється принаймні в одній фінальній вершині.

Серед бінарних дерев найпростішими є ті, у котрих кожний кандидат приписаний рівно одній вершині. Назвемо їх деревами без повторних виключень .

Лема 2.1

(а) Якщо А складається з трьох кандидатів , то дерево після послідовного виключення є єдиним безповторним деревом . Відповідне правило голосування оптимальне за Парето (при нашій умові , що всі порівняння по більшості суворі ).

(b ) Якщо А складається з чотирьох кандидатів , тобто тільки два безповторних дерева: послідовне виключення і рівнобіжне виключення . Перше з них порушує оптимальність за Парето , а останнє - ні .

(c ) Якщо А містить п'ять або більше кандидатів , то будь-яке виключення по безповторному дереву призводить до обрання кандидата для деяких профілі,в що домінується за Парето .

Існує бінарне дерево, визначене для довільної кількості учасників, що дозволяє уникнути обох цих небезпек. Відповідні послідовні виключення породжують оптимальне за Парето, анонімне і монотонне правило голосування. Це дерево називається деревом багатоетапного виключення .

Для кожного конкретного упорядкування кандидатів існує по одному такому дереву. Позначимо через Г_p (1,2,... ,р) дерево, що відповідає порядку A ={1,2,... ,р }. Визначимо його індуктивно за розміром А:

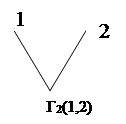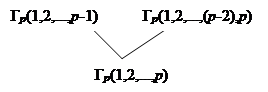Так, для трьох і чотирьох кандидатів одержуємо:

Г4 (1,2,3)

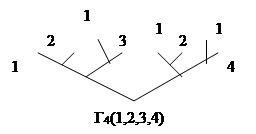При р кандидатах утворюються 2p-l фінальні вершини; кандидат 1 приписаний 2p-2 фінальним вершинам, а кандидат р тільки однієї. Тим не менше для обрання навіть кандидату р потрібно перемогти в р -1 дуелях (хоча йому можливо прийдеться по декілька разів зіткнутися з тим самим опонентом).

Хоча дерево багатоетапного виключення велике, його рішення (тобто обчислення кандидата, що виграє) може бути отримане за допомогою дуже простого алгоритму

Теорема 2.4 (Шепсл і Вейнгаст [1984]).

Задані дерево багатоетапного виключення Г_p (1,2,... ,р) і профіль переваги, що відповідає мажоритарному турніру Т. Кандидат а ^* може бути знайдений за таким алгоритмом:

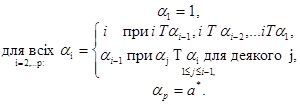(12)

Наслідок теореми 2.4. Кандидат а , що вибирається по дереву багатоетапного виключення з турніром Т , задовольняє умові:

для будь-якого b ÎА , b ¹а:

{аТb } і/або {для деякого с , аТс і сTb }. (14)

Зокрема, а оптимальний за Парето . Більш того , дерево багатоетапного виключення породжує монотонний метод голосування .

Серед заможних за Кондорсе правил голосування ми виявили три методи, що задовольняють основним вимогам оптимальності за Парето, анонімності і монотонності: множина переможців за Коплендом, множина переможців за Сімпсоном і дерево багатоетапного виключення. Перші два нейтральні, але можуть виділяти декількох переможців (додаткове правило при рівності очок порушить нейтральність). Зауважимо, що переможець при багатоетапному виключенні знаходиться швидше, оскільки алгоритм (12) у середньому потребує порівняння не більше половини від усіх p (p-l ) пар. У той же час для визначення переможців за Коплендом і Сімпсоном потрібно провести весь турнір порівнянь за правилом більшості.

3 Математичні методи розв’язку

У попередньому розділі були описані методи підрахунку очок і основні вимоги до них. Порівняємо ці методи.

Як було зазначено, найлегшим серед них, але й найгіршим, є правило відносної більшості. Можна переконатись, що насправді воно суперечить думці більшості. Тому воно не може бути вибране для комп’ютерної реалізації.

Як Борда, так і Кондорсе зауважили, що правило відносної більшості може призводити до обрання поганого кандидата, точніше такого кандидата, що у парному порівнянні за правилом більшості програє будь-якому іншому кандидату.

Для того щоб перебороти цю хибу, Кондорсе і Борда запропонували відмовитися від правила відносної більшості, причому кожний із них запропонував своє правило замість даного. Кондорсе запропонував вибирати кандидата, що перемагає будь-якого іншого кандидата в парному порівнянні, якщо такий переможець за Кондорсе існує. Борда запропонував приписати очко кожному кандидату, який лінійно зростає у залежності від його рангу в перевазі виборця. Потім він запропонував обрати кандидата, що одержав найбільшу сумарну кількість очок в усіх виборців. Ці дві ідеї породжують два найбільше важливих сімейств правил голосування.

Результати цих правил голосування можуть сильно відрізнятися за властивостями. Однією із таких властивостей є аксіома монотонності. Правило голосування називається монотонним, якщо кандидат залишається обраним при посиленні його підтримки (тобто коли відносна позиція даного кандидата у чиїхось перевагах поліпшується, а відносні позиції інших кандидатів не змінюються). Всі методи підрахунку очок є монотонними, але деякі відомі методи, що виникають із підрахунку очок, не є такими. Прикладами таких правил служать дуже популярне правило відносної більшості з вибуванням і метод альтернативних голосів.

Є дві аксіоми, що призводять до критики заможних за Кондорсе правил (оскільки дані правила порушують ці аксіоми). З іншого боку, на цих аксіомах заснована характеризація методу підрахунку очок. Ці аксіоми порівнюють кандидатів, обраних різноманітними групами виборців. Вони називаються властивостями поповнення й участі. Поповнення означає, що якщо дві групи виборців , що не перетинаються, (наприклад, сенат і палата представників) обирають того самого кандидата а , то об'єднання цих двох виборчих органів підтвердить обрання а . Участь означає, що виборець не може виграти, утримуючись від голосування, у порівнянні з можливістю брати участь у голосуванні і висловити свої переваги. Будь-яке заможне за Кондорсе правило порушує обидві ці аксіоми. На противагу цьому правила підрахунку очок характеризуються властивістю поповнення (теорема Янга) і задовольняють аксіомі участі. Теорема Янга в даний час є найістотнішим доказом у підтримку методів підрахунку очок, зокрема системи очок Борда.