Реферат: Моделі систем масового обслуговування. Класифікація систем масового обслуговування
Для прикладу (мал. 1) маємо:
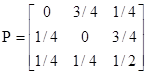 .
.
і рішення матричного рівняння зводиться до рішення системи трьох рівнянь:
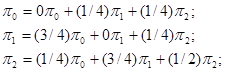
Коефіцієнти першого рівняння в цій системі доповнюють до одиниці суму коефіцієнтів другого і третього рівнянь; це свідчить про лінійну залежність між ними. Тому для вирішення системи рівнянь потрібно ввести додаткову нормуючу умову. В даному прикладі: ![]() .
.
Вирішуючи систему отриманих рівнянь, маємо:
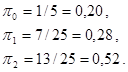
Рівняння для вірогідності досягнення стану в перехідному режимі вирішити значно важче. Деякого спрощення можна досягти, використовуючи z – перетворення. Застосуємо його до рівняння для перехідної вірогідності
![]() .
.
Позначаючи відповідні перетворення, отримаємо: ![]() .
.
Всі отримані тут математичні результати відносилися до однорідних Марківських процесів, де вірогідність переходів не залежить від часу. В більш загальному випадку така залежність має місце.
Розглянемо вірогідність переходу системи із стану i на m-том кроці в стан j на n-том кроці для n > m.
Можна показати, що ця вірогідність зв'язана між собою, так званим рівняннями Чепмена-Колмогорова. (Chapman – Kolmogorov)
![]() .
.
Для однорідних ланцюгів Маркова ці рівняння спрощуються оскільки
![]() .
.
І зводяться до аналізованих вище.
Безперервні ланцюги Маркова
Випадковий процес X(t) з дискретною безліччю значень утворює безперервний ланцюг Маркова, якщо
![]() .
.
Майбутні стани залежать від минулого тільки через поточний стан. Для безперервний ланцюгів Маркова основним також є рівняння Чепмена – Колмогорова, для однорідного ланцюга має вигляд: ![]() .
.
Тут матриця H(t)= [pij(t)] – матриця вірогідності переходу із стану i в стан j у момент часу t, а матриця Q називається «матрицею интенсивностей переходів». Її елементи мають наступний сенс: якщо у момент часу t система знаходилася в стані Ei, то вірогідність переходу протягом проміжку часу (t,t+Дt) в довільний стан Ej задається величиною qij(t)Дt + о(Дt), а вірогідність відходу із стану Ei величиною -qiiДt + про(Дt).
Таким чином, інтенсивності переходів можна обчислювати як відповідні межі при прагненні до нуля тривалості тимчасового інтервалу.
Найважливішим для подальшого використовування є клас безперервних ланцюгів Маркова званих «процесами загибелі – розмноження» ( Birth – death process). Для таких систем із стану до можливі переходи тільки в стани до, k‑1 і k+1 в наступні моменти часу:
· у момент t об'єм популяції був рівний до і протягом часу (t, t+Дt) не відбулося зміни стану
· у момент t об'єм популяції був рівний k‑1 і протягом часу (t, t+Дt) народився один член популяції
· у момент часу t об'єм популяції був рівний k+1 і протягом часу (t, t+Дt) загинув один член популяції.
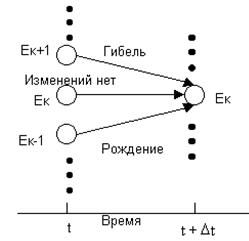
Мал. 1. Можливі переходи в стан Тіньк