Реферат: Моделі систем масового обслуговування. Класифікація систем масового обслуговування

В загальному випадку ясно, що із збільшенням числа вимог росте час очікування. Встановимо співвідношення між середнім числом вимог в системі, інтенсивністю потоку і середнього часу перебування в системі. Позначимо число поступають в проміжку часу (0, t ) вимог як функцію часу б(t).

Число витікаючих з системи заявок (обслужених) на цьому інтервалі позначимо д(t). На малюнку 4 показані приклади функціональної залежності цих двох випадкових процесів від часу.

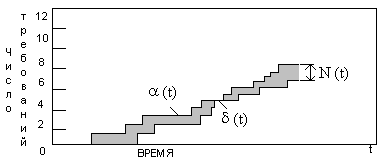
Мал. 4. Залежність між середнім числом вимог в системі, інтенсивністю потоку і середнім часу перебування в системі

Число вимог, що знаходяться в системі у момент t буде рівний:

.

Площа між двома даними кривими від 0 до t – дає загальний час, проведений всіма заявками в системі за час t.

Позначимо цю накопичену величину г(t). Якщо інтенсивність вхідного потоку рівна л, а середня інтенсивність за час t: , той час, проведений однією заявкою в системі, усереднене по всіх заявках буде рівне:

.

Нарешті, визначимо середнє число вимог в системі в проміжку (0, t): .

З останніх трьох рівнянь виходить, що: (де ).

Якщо в СМО існує стаціонарний режим, то при t>?, матимуть місце співвідношення:

Останнє співвідношення означає, що середнє число заявок в системі рівно твору інтенсивності надходження вимог в систему на середній час перебування в системі. При цьому не накладається ніяких обмежень на розподіли вхідного потоку і часу обслуговування. Вперше доказ цього факту дав Дж. Литтл і це співвідношення носить назву формула Літтла.

Цікаво, що як СМО можна розглянути тільки чергу із заявок в буфері. Тоді формула Літтла придбаває інше значення – середня довжина черги рівна твору інтенсивності вхідного потоку заявок на середній час очікування в черзі: .

Якщо навпаки розглядати СМО тільки як сервери, то формула Літтла дає:

,

де – середнє число заявок в серверах, а – середній час обробки в сервері.

У будь-якому випадку: .

Одним з основних параметрів, які використовуються при описі СМО, є коефіцієнт використовування (utilization factor). Це фундаментальний параметр, оскільки він визначається як відношення інтенсивності вхідного потоку до пропускної спроможності системи. Оскільки пропускна спроможність СМО містить m серверів може бути визначений як: , то коефіцієнт використовування може бути визначений як .

Неважко бачити, що коефіцієнт використовування рівний в точності інтенсивності навантаження, якщо СМО з одним сервером і в m раз менше для систем з m серверами. Величина коефіцієнта використовування рівна середньому значенню від частки зайнятих серверів і .

Якщо в СМО типа G/G/1 існує стаціонарний режим і можна визначити вірогідність того, що в деякий випадковий момент сервер буде вільний, то .