Реферат: Моделі систем масового обслуговування. Класифікація систем масового обслуговування
![]() .
.
Визначимо граничні і нормуючі умови:
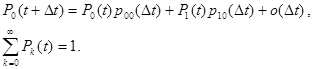
Виразимо вірогідність переходів за інтервал Дt через інтенсивності
Віри(+1)=лk Дt+o(Дt); Віри(-1)=мk Дt+o(Дt).
Вірогідність нуля народжень 1 – лkДt+o(Дt), а нуля загибелі 1 – мkДt+o(Дt).
Таким чином, вірогідність того, що стан до збережеться незмінним, буде рівна твору [1 – лkДt+o(Дt)] [1 – мkДt+o(Дt)].
Тоді рівняння Чепмена-Колмогорованабувають вигляд
![]()
Розкриваючи дужки і проводячи розподіл на Дt, отримаємо:
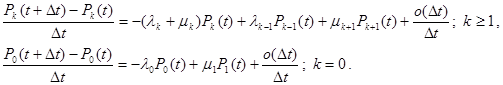
В межі виходить система диференціально-різницевих рівнянь, рішення якої гратимуть важливу роль для практичних задач.
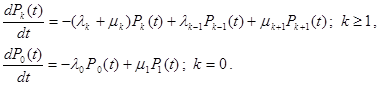
У відповідність цій системі рівнянь можна поставити наочну діаграму интенсивностей переходів, яка аналогічна діаграмі переходів для дискретних ланцюгів Маркова (Мал. 2)
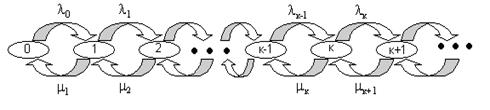
Мал. 2. Діаграма интенсивностей переходів для процесу розмноження і загибелі
Овалам тут відповідають дискретні стани, а стрілки визначають інтенсивності потоків вірогідності (а не вірогідність!) переходів від одного стану до іншого.
Має місце своєрідний «закон збереження»:
Різниця між сумою интенсивностей, з якою система потрапляє в стан до і сумою интенсивностей, з якою система покидає цей стан повинна дорівнювати інтенсивності зміни потоку в цей стан (похідної за часом).
Застосування закону збереження дозволяє одержувати рівняння для будь-якої підсистеми Марківського ланцюга типу процесу «загибелі-розмноження. Особливо ефективною виявляється побудова рішень в стаціонарному, сталому режимі, коли можна вважати що вірогідність в довільний, достатньо віддалений момент часу, залишаються постійними.
Прирівнюючи похідну за часом нулю, одержуємо систему різницевих рівнянь
![]()
Вважаючи, що інтенсивності л‑1 =л-2 = л‑3=.0; м0 = м‑1 = м‑2 = м‑3=.=0, друге рівняння виписувати не буде окремо далі потрібно. Отже, стаціонарний режим в ланцюзі Маркова описуватиметься системою різницевих рівнянь і умовою нормування для вірогідності
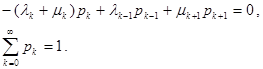
Неважко бачити, що ці рівняння легко виводяться із закону збереження интенсивностей вірогідності. В стаціонарному режимі різниця потоків рівна нулю і отримані вище рівняння придбавають значення рівнянь рівноваги або балансу, як їх і називають.
![]() .
.
Інтенсивність потоку вірогідності в стан до рівна інтенсивності потоку з цього стану.
Вирішувати рівняння балансу можна, спочатку визначивши при до =0 значення
![]() .
.