Реферат: Модели системы кровообращения

Общая длина моделируемых артерий составляет 720 см.

Полагается, что вязкость крови равна 3*10^-2 пуаз и плотность крови составляет 1,05 г/см³ .

Модуль упругости Юнга был сначала принят равным 4*10⁶ г*с^-1 *сек^-2 .

Конструкция модели.

Требования, предъявляемые к точности. Продольный импеданс. По радиусу отдельного сегмента в можно рассчитать число сопротивлений и индуктивностей, а корректирующей сети для этого сегмента в зависимости от точности, необходимой для самых высоких из интересующих нас частот (15 Гц). Испытания были проведены в широкой области частот.

Трансверсальный импеданс, т.е. значение емкости, реализовывался с погрешностью в пределах 3%.

Исходя из задаваемой степени точности для продольного и трансверсального импедансов индивидуальных сегментов, были определены допуски для характерных элементов, с помощью которых реализуются эти импедансы. Для этого использовались сердечники высокой магнитной проницаемостью, так как они позволяют сконструировать почти чистую индуктивность, которая необходима в корректирующей сети.

Сопротивления, меньшие 5 Ом, были выполнены из специальной проволоки, другие сопротивления и емкости делались из деталей, имеющихся в продаже.

Каждый сегмент был смонтирован в отдельной алюминиевой коробке, и все эти коробки были смонтированы на стойках (всего три стойки). Периферические сопротивления, представленные потенциометрами, устанавливались внутри коробок каждого концевого сегмента. В каждом сегменте записывались показания расхода (тока) посредством включения измеряющего прибора в отдельные доступные места проводки.

После соединения всех элементов измерялся продольный импеданс в широкой области частот. Эти измеренные значения сравнивались с ожидаемыми значениями импеданса, которые подсчитывались непосредственно с использованием таблиц, данных Уомерсли. Проверялся также трансверсальный импеданс. В некоторых случаях указанные импедансы необходимо было регулировать, чтобы учесть емкость проводки.

Ошибка, вводимая агрегированием, может быть уменьшена, особенно для высоких частот, посредством использования симметричной сети (П) вместо несимметричной (┐). Характеристический импеданс Z₀ ┐и волновое число γ┐ однородной линии передачи, агрегированной в конечные сегменты, могут быть выражены как функции характеристического импеданса Z₀ и волнового числа γ реальной линии передачи (с бесконечно короткими сегментами). Возникающая за счет агрегирования ошибка в значении Z₀ ┐имеет порядок γΔz/2, а в значении γ┐ - порядок (γΔz/2) ² , где Δz - длина сегмента. Для симметричной сети (П) нами найдено, что ошибка как в Z_0П , так и в γ_П имеет порядок (γΔz/2) ² . В нашей модели величина γΔz выбиралась так, чтобы она была приблизительно постоянна по всей системе, т.е. длина сегментов аорты меньше, чем периферических сосудов. Ошибки из-за агрегирования увеличиваются с частотой. При частоте 15 Гц γΔz величина приблизительно равна 0,5, и ясно, что это дает ошибку в величине Z₀ ┐около 25%, а в величине Z_0П - только около 6%; следовательно, симметричная сеть является лучшей аппроксимацией по сравнению с несимметрично сетью.

Оценка модели

Симметричная сеть была введена как следующее улучшение, и в качестве примеры был приведен входной импеданс артериального древа организма в целом. Отсюда модно заключить, что в отношении входного импеданса, который "ощущается" левым желудочком, длина сегментов достаточно мала для интересующей нас области частот.

Недостаточное количество данных не позволяет приписать основные локальные значения модуля Юнга различным артериям, представленным в исходной модели. Поэтому в качестве рабочей гипотезы было принято, что среднее значение модуля Юнга можно использовать для всех артерий древа.

Измерения Бергеля, Лиройда и Тейлора показали, что модуль Юнга для различных артерий различен. К тому же модуль Юнга зависит от частоты и величины механических напряжений.

Поводя итог, модно сказать, что с точки зрения влияния на входной импеданс улучшения весьма малы. По-видимому, входной импеданс системы в целом совершенно нечувствителен к рукавному эффекту, симметричной сети или даже к упругому сужению. Также он не зависит практически от периферического сопротивления. [4]

В качестве примера вполне работоспособной модели второго класса с разбиением, близким к оптимальному, можно рассмотреть модель кровообращения, представленную на рисунке 1.

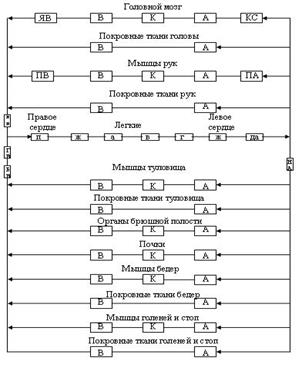
Рис.1. Блок-схема модели кровообращения

Обозначения на рисунке:

А - артерии, В - вены, К - капилляры, Ж - желудочек, П - предсердие, КС - каротидные синусы, ЯВ - яремные вены, ДА - дуга аорты, НА - нисуолящая аорта, ПА - подключичная артерия, ВВ - верхняя полая вена, ГВ и БВ - грудная и брюшная нижние полые вены.

Насосная функция сердца описывается уравнением:

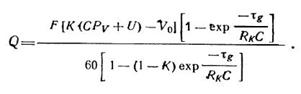
Здесь Q- объемный кровоток на выходе желудочка

F- частота сердечных сокращений

K- сократительная способность сердца

C- диастолическая растяжимость желудочка

P_v - венозное давление на входе сердца

U- ненапряженный объем желудочка при P=0

V_o - свободный член статической аппроксимации Q=Q (P_v ).