Реферат: Модели системы кровообращения

где a и b - константы. Объем крови V_i =V_i (t) для i-го участка системы задается уравнением баланса

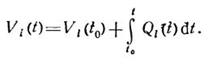
Здесь Q_i - алгебраическая сумма по j объемных скоростей кровообмена q_ij между i-м участком и всеми остальными, причем q_ij ≡0, если j-ый участок непосредственно не сообщается с i-ым. В противном случае принимается, что

где P_i - суммарное давление крови на i-ом участке,

R_i - сопротивление кровотоку на этом участке.

В модели учитывается, что в некоторых периферических венах при падении давления сечение приобретает эллиптическую форму. Для этих сосудов принималось:

А для сосудов верхней половины тела:

Здесь - сопротивление сосуда в условиях, когда его объем равен Ui- ненапряженному объему;

- сопротивление сосуда при горизонтальном положении тела, когда объем сосуда равен .

Зависимость трансмурального давления (давления, обусловленного упругостью сосудистой стенки) от рассматриваемых переменных имеет вид:

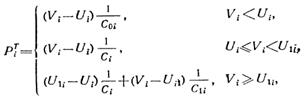
где - объемная податливость сосудов соответственно в области отрицательного, низкого положительного и высоко положительного давлений;

- параметр аппроксимации.

Суммарное давление в i-ом сосуде равно:

Здесь - гидростатическое давление, пропорциональное величине действующей перегрузки и отсчитываемое от выбранного нулевого уровня (обычно от уровня нижней точки тела или уровня сердца);

- давление в тканях, окружающих i-ый участок сосудистого русла:

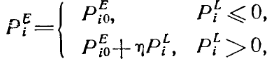
причем - избыточное давление на поверхности тела в зоне i-го элемента модели;

- внесосудистое давление в тканях в условиях физиологической нормы

ŋ - коэффициент передачи давления, ŋ ≤1.

Эти уравнения полностью описывают биомеханическую модель кровообращения в условиях измененной весомости и перепадов давления по телу. Для учета физиологических компенсаторных реакций в модель дополнительно вводится контур автоматического регулирования давлений крови в зонах аорты и каротидных синусов. В качестве регулируемых параметров приняты частота и сила сердечных сокращений, а также сопротивление, податливость и ненапряженный объем участков сосудистого русла. Отклонение давлений в контролируемых зонах от исходных "нормальных" значений (давления в покое в позе "лежа") приводит к включению схемы пропорционального регулирования вышеперечисленных параметров, причем для каждого из них справедливо уравнение

где Δα - отклонение регулируемого параметра от исходного значения

k_α - коэффициент усиления;