. (4)

Підбирають функцію і число таким, щоб імовірнісні характеристики отриманого ВЕ збігалися з імовірнісними характеристиками оригіналу, що моделюється. Існують різні критерії близькості імовірнісних характеристик ВЕ - оригіналу і ВЕ, отриманого при моделюванні, зокрема, критерій Пірсона, критерій Колмогорова.

2. Моделювання випадкових величин із заданими ймовірнісними характеристиками

Оскільки моделювання випадкових процесів на ЕОМ зводиться до моделювання послідовності випадкових величин із заданими ймовірнісними характеристиками, спочатку розглянемо особливості моделювання деяких випадкових величин.

Моделювання випадкових величин, що приймають дискретні значення

Розглянемо моделювання випадкових величин , що приймають дискретних значень із заданими ймовірностями ()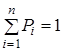. Моделювання таких ВВ може бути зведене до моделювання повної групи незалежних подій, які відбуваються з імовірностями . Для цього використовується датчик БВВ із математичною моделлю .

Введемо систему таких підмножин , щоб їх можна було розглядати як повну групу незалежних подій на . При цьому повинні задовольнятись умови 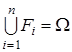; ; 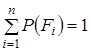. Визначимо ці підмножини так

, (5)

де і - це межі інтервалів, які визначаються за формулою

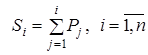, причому . (6)

Зважаючи на те, що БВВ розподілена рівномірно на інтервалі , імовірності підмножин визначаються через щільність розподілу БВВ відповідним спввідношенням

. (7)

Це означає, що імовірність попадання значення БВВ в інтервал дорівнює довжині цього інтервалу (рис.3).

Рисунок 3 - Геометричне пояснення моделювання групи незалежних подій з допомогою БВВ

Таким чином, моделювання ВВ , яка приймає дискретні значення, полягає у виборі значення БВВ за допомогою генератора, перевірки попадання значення БВВ до однієї з підмножин і винесенні рішення про те, що модельоване ВВ приймає значення

, (8)

де - це характеристична функція множини. (9)

Моделювання випадкових величин із заданими щільностями імовірностей методом обернених функцій

Розглянемо моделювання ВВ із заданою щільністю ймовірності та функцією розподілу

. (10)

Якщо функція є строго монотонно зростаючою, то із рівняння можна знайти обернену функцію

. (11)

Підставивши замість БВВ , можна одержати алгоритм моделювання ВВ із заданим розподілом:

. (12)

Таким чином, для моделювання на ЕОМ ВВ із заданою щільністю ймовірності, потрібно виконати такі операції:

знайти функцію розподілу, користуючись заданою щільністю ймовірності;

знайти функцію, що буде оберненою до функції розподілу;

одержувати реалізації БВВ ;

обчислювати значення ВВ як значення знайденої функції .

Виконуючи ці операції - разів, одержимо вибірку реалізацій . Скориставшись нею, можна побудувати гістограму розподілу і порівняти її з заданою щільністю ймовірності.

Даний метод моделювання має недоліки тому, що не завжди вдається аналітично розрахувати для заданої щільності ймовірностей інтеграл для одержання , і не для всякої функції розподілу вдається одержати обернену функцію.

Моделювання випадкових величин із заданими щільностями імовірностей методом суперпозиції