Реферат: Морфологический анализ цветных (спектрозональных) изображений
в котором почти для всех ![]() ,
, ![]() , - m-измеримые функции на поле зрения X , такие, что
, - m-измеримые функции на поле зрения X , такие, что
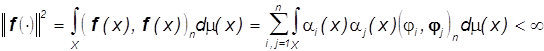 .
.
Цветные изображения образуют подкласс функций ![]() лебеговского класса
лебеговского класса ![]() функций
функций ![]() . Класс цветных изображений обозначим LE ,n .
. Класс цветных изображений обозначим LE ,n .
Впрочем, для упрощения терминологии далее любой элемент ![]() называется цветным изображением, а условие
называется цветным изображением, а условие
![]() (2*)
(2*)
условием физичности изображений f (Ч).
Если f (Ч) - цветное изображение (2), то ![]() , как нетрудно проверить, - черно-белое изображение [2], т.е.
, как нетрудно проверить, - черно-белое изображение [2], т.е. 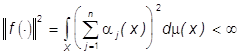 ,
, ![]() . Изображение
. Изображение ![]() , назовем черно-белым вариантом цветного изображения f (Ч), а цветное изображение
, назовем черно-белым вариантом цветного изображения f (Ч), а цветное изображение ![]() , f(x)0 , xОX - цветом изображения f (Ч) . В точках множества В={xОX : f (x )=0} черного цвета j (x ), xО В, - произвольные векторы из
, f(x)0 , xОX - цветом изображения f (Ч) . В точках множества В={xОX : f (x )=0} черного цвета j (x ), xО В, - произвольные векторы из ![]() , удовлетворяющие условию: яркость j (x )=1. Черно-белым вариантом цветного изображения f (Ч) будем также называть цветное изображение b (Ч), имеющее в каждой точке Х ту же яркость, что и f (Ч) , b(x)=f(x), xОX , и белый цвет, b (x)=b (x)/b(x)=b , xОX.
, удовлетворяющие условию: яркость j (x )=1. Черно-белым вариантом цветного изображения f (Ч) будем также называть цветное изображение b (Ч), имеющее в каждой точке Х ту же яркость, что и f (Ч) , b(x)=f(x), xОX , и белый цвет, b (x)=b (x)/b(x)=b , xОX.
3. Форма цветного изображения.
Понятие формы изображения призвано охарактеризовать форму изображенных объектов в терминах характерности изображений, инвариантных относительно определенного класса преобразований изображения, моделирующих меняющиеся условия его регистрации. Например, довольно часто может меняться освещение сцены, в частности, при практически неизменном спектральном составе может радикально изменяться распределение интенсивности освещения сцены. Такие изменения освещения в формуле (2**) выражаются преобразованием ![]() , в котором множитель k(x) модулирует яркость изображения
, в котором множитель k(x) модулирует яркость изображения ![]() в каждой точке
в каждой точке ![]() при неизменном распределении цвета. При этом в каждой точке
при неизменном распределении цвета. При этом в каждой точке ![]() у вектора f (x) может измениться длина, но направление останется неизменным.
у вектора f (x) может измениться длина, но направление останется неизменным.
Нередко изменение распределения интенсивности освещения сопровождается значительным изменением и его спектрального состава, но - пространственно однородным, одним и тем же в пределах всей изображаемой сцены. Поскольку между спектром излучения e и цветом j нет взаимно однозначного соответствия, модель сопутствующего преобразования изображения f (x) в терминах преобразования его цвета j (Ч). Для этого определим отображение A (Ч):![]() , ставящее в соответствие каждому вектору цвета
, ставящее в соответствие каждому вектору цвета ![]() подмножество поля зрения
подмножество поля зрения ![]() в точках которого изображение
в точках которого изображение ![]() , имеет постоянный цвет
, имеет постоянный цвет ![]() .
.
Пусть при рассматриваемом изменении освещения ![]() и, соответственно,
и, соответственно, ![]() ; предлагаемая модель преобразования изображения состоит в том, что цвет
; предлагаемая модель преобразования изображения состоит в том, что цвет ![]() преобразованного изображения должен быть также постоянным на каждом множестве A (j ), хотя, вообще говоря, - другим, отличным от j. Характекрным в данном случае является тот факт, что равенство
преобразованного изображения должен быть также постоянным на каждом множестве A (j ), хотя, вообще говоря, - другим, отличным от j. Характекрным в данном случае является тот факт, что равенство ![]() влечет
влечет ![]() . Если
. Если ![]() - самое детальное изображение сцены, то, вообще говоря, на различных множествах A (jў ) и A (j ) цвет изображения
- самое детальное изображение сцены, то, вообще говоря, на различных множествах A (jў ) и A (j ) цвет изображения ![]() может оказаться одинаковым [5] .
может оказаться одинаковым [5] .
Как правило, следует учитывать непостоянство оптических характеристик сцены и т.д. Во всех случаях форма изображения должна быть инвариантна относительно преобразования из выделенного класса и, более того, должна определять изображение с точностью до произвольного преобразования из этого класса.
Для определения понятия формы цветного изображения f (Ч) на ![]() удобно ввести частичный порядок p , т.е. бинарное отношение, удовлетворяющее условиям: 1)
удобно ввести частичный порядок p , т.е. бинарное отношение, удовлетворяющее условиям: 1)![]() , 2)
, 2) ![]() ,
, ![]() , то
, то ![]() ,
, ![]() ; отношение p должно быть согласованным с определением цветного изображения (с условием физичности), а именно,
; отношение p должно быть согласованным с определением цветного изображения (с условием физичности), а именно, ![]() , если
, если ![]() . Отношение p интерпретируется аналогично тому, как это принято в черно-белой морфологии[2], а именно,
. Отношение p интерпретируется аналогично тому, как это принято в черно-белой морфологии[2], а именно, ![]() означает, что изображения f (Ч) и g (Ч) сравнимы по форме, причем форма g (Ч) не сложнее, чем форма f (Ч) . Если
означает, что изображения f (Ч) и g (Ч) сравнимы по форме, причем форма g (Ч) не сложнее, чем форма f (Ч) . Если ![]() и
и ![]() , то f (Ч) и g (Ч) назовем совпадающими по форме (изоморфными), f (Ч) ~ g (Ч) . Например, если f (Ч) и g (Ч) - изображения одной и той же сцены, то g (Ч) , грубо говоря, характеризует форму изображенных объектов не точнее (подробнее, детальнее), чем f (Ч) , если
, то f (Ч) и g (Ч) назовем совпадающими по форме (изоморфными), f (Ч) ~ g (Ч) . Например, если f (Ч) и g (Ч) - изображения одной и той же сцены, то g (Ч) , грубо говоря, характеризует форму изображенных объектов не точнее (подробнее, детальнее), чем f (Ч) , если ![]() .
.
В рассматриваемом выше примере преобразования изображений ![]() , если между множествами A (j ),
, если между множествами A (j ),![]() и Aў (jў ),
и Aў (jў ),![]() существует взаимно-однозначное соответствие, т.е., если существует функция
существует взаимно-однозначное соответствие, т.е., если существует функция ![]() , такая, что Aў (jў (j ))= A (j ),
, такая, что Aў (jў (j ))= A (j ),![]() , причем
, причем![]() , если
, если ![]() . В этом случае равенства
. В этом случае равенства ![]() и
и ![]() эквивалентны,
эквивалентны, ![]() и
и ![]() изоморфны и одинаково детально характеризуют сцену, хотя и в разных цветах.
изоморфны и одинаково детально характеризуют сцену, хотя и в разных цветах.
Если же ![]() не взаимно однозначно, то Aў (jў )=U A (j ) и
не взаимно однозначно, то Aў (jў )=U A (j ) и ![]() . В этом случае равенство
. В этом случае равенство ![]() влечет
влечет ![]() (но не эквивалентно)
(но не эквивалентно) ![]() ,
, ![]() передает, вообще говоря, не все детали сцены, представленные в
передает, вообще говоря, не все детали сцены, представленные в ![]() .
.
Пусть, скажем, g (Ч) - черно-белый вариант f (Ч) , т.е. g(x)=f(x) и g (x)/g(x)= b , x ОX . Если преобразование ![]() - следствие изменившихся условий регистрации изображения, то, естественно,
- следствие изменившихся условий регистрации изображения, то, естественно, ![]() . Аналогично, если f (Ч), g (Ч) - изображения одной и той же сцены, но в g (Ч), вследствие неисправности выходные сигналы некоторых датчиков равны нулю, то
. Аналогично, если f (Ч), g (Ч) - изображения одной и той же сцены, но в g (Ч), вследствие неисправности выходные сигналы некоторых датчиков равны нулю, то ![]() . Пусть F - некоторая полугруппа преобразований
. Пусть F - некоторая полугруппа преобразований ![]() , тогда для любого преобразования F ОF
, тогда для любого преобразования F ОF ![]() , поскольку, если некоторые детали формы объекта не отражены в изображении f (Ч), то они, тем более, не будут отражены в g (Ч).
, поскольку, если некоторые детали формы объекта не отражены в изображении f (Ч), то они, тем более, не будут отражены в g (Ч).
Формой ![]() изображения f (Ч) назовем множество изображений
изображения f (Ч) назовем множество изображений ![]() , форма которых не сложнее, чем форма f` (Ч), и их пределов в
, форма которых не сложнее, чем форма f` (Ч), и их пределов в ![]() (черта символизирует замыкание в
(черта символизирует замыкание в ![]() ). Формой изображения f (Ч) в широком смысле назовем минимальное линейное подпространство
). Формой изображения f (Ч) в широком смысле назовем минимальное линейное подпространство ![]() , содержащее
, содержащее ![]() . Если считать, что
. Если считать, что ![]() для любого изображения
для любого изображения ![]() , то это будет означать, что отношение p непрерывно относительно сходимости в
, то это будет означать, что отношение p непрерывно относительно сходимости в ![]() в том смысле, что
в том смысле, что ![]() .
.
Рассмотрим теперь более подробно понятие формы для некоторых характерных классов изображений и их преобразований.
4. Форма кусочно-постоянного (мозаичного) цветного изображения.
Во многих практически важных задачах форма объекта на изображении может быть охарактеризована специальной структурой излучения, достигающего поле зрения X в виде ![]() здесь
здесь ![]() - индикаторные функции непересекающихся подмножеств Аi , i=1,…...,N, положительной меры поля зрения Х , на каждом из которых функции
- индикаторные функции непересекающихся подмножеств Аi , i=1,…...,N, положительной меры поля зрения Х , на каждом из которых функции  ,
, ![]() , j =1,...,n , i =1,...,N , непрерывны. Поскольку согласно лемме 2
, j =1,...,n , i =1,...,N , непрерывны. Поскольку согласно лемме 2
![]()

![]() , (3)
, (3)
то цветное изображение fe (Ч), такого объекта характеризует его форму непрерывным распределением яркости и цвета на каждом подмножестве Ai , i =1,...,N . Для изображения ![]() ,
, ![]() где
где ![]() , также характерно напрерывное распределение яркости и цвета на каждом Ai , если
, также характерно напрерывное распределение яркости и цвета на каждом Ai , если ![]() , - непрерывные функции.
, - непрерывные функции.
Если, в частности, цвет и яркость ![]() постоянны на Ai , i =1,...,N , то это верно и для всякого изображения
постоянны на Ai , i =1,...,N , то это верно и для всякого изображения ![]() , если
, если ![]() не зависит явно от
не зависит явно от ![]() . Для такого изображения примем следующее представление:
. Для такого изображения примем следующее представление:
![]() , (4)
, (4)
его черно-белый вариант
![]() (4*)
(4*)
на каждом Ai имеет постоянную яркость ![]() , и цвет изображения (4)
, и цвет изображения (4)
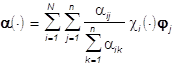 (4**)
(4**)
не меняется на Ai и равен 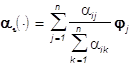 , i =1,...,N .
, i =1,...,N .