Реферат: Морфологический анализ цветных (спектрозональных) изображений

Пытьев Ю.П.

Московский государственный университет, Москва, Россия

1. Введение

Хорошо известно, что изображения одной и той же сцены, полученные при различных условиях освещения и(или) измененных [1] оптических свойствах объектов могут отличаться радикально. Это обстоятельство порождает значительные трудности в прикладных задачах анализа и интерпретации изображений реальных сцен, в которых решение должно не зависеть от условий регистрации изображений. Речь идет, например, о задачах выделения неизвестного объекта на фоне известной местности, известного объекта на произвольном фоне при неконтролируемых условиях освещения, о задаче совмещения изображенний одной и той же сцены, полученных в различных спектральных диапазонах и т.д.

Методы морфологического анализа, разработанные более десяти лет тому назад, [1-5], для решения перечисленных задач, были в основном ориентированы для применения к черно-белым изображениям [2] и оказались достаточно эффективными, [5-11].

Между тем, по меньшей мере два обстоятельства указывают на целесообразность разработки морфологических методов анализа цветных изображений. Во-первых, в задаче обнаружения и выделения объекта последний, как правило, прежде всего цветом отличается от фона. Во-вторых, описание формы изображения в терминах цвета позволит практически устранить эффект теней и влияние неопределенности в пространственном распределении интенсивности спектрально однородного освещения.

2. Цвет и яркость спектозонального изображения.

Рассмотрим некоторые аспекты теории цвета так называемых многоспектральных (спектрозональных, [13]) изображений, аналогичной классической колориметрии [12]. Будем считать заданными n детекторов излучения со спектральными чувствительностями j =1,2,...,n , где l (0,Ґ) - длина волны излучения. Их выходные сигналы, отвечающие потоку излучения со спектральной плотностью e (l )0, lО (0,Ґ), далее называемой излучением, образуют вектор , w (Ч)=. Определим суммарную спектральную чувствительность детекторов , lО (0,Ґ), и соответствующий суммарный сигнал назовем яркостью излучения e (Ч). Вектор назовем цветом излучения e (Ч). Если цвет e (Ч) и само излучение назовем черным . Поскольку равенства и эквивалентны, равенство имеет смысл и для черного цвета, причем в этом случае - произвольный вектор, яркость оторого равна единице. Излучение e (Ч) назовем белым и его цвет обозначим если отвечающие ему выходные сигналы всех детекторов одинаковы:

.

Векторы , и , , удобно считать элементами n -мерного линейного пространства . Векторы f _e , соответствующие различным излучениям e (Ч), содержатся в конусе . Концы векторов содержатся в множестве , где П - гиперплоскость .

Далее предполагается, что всякое излучение , где E - выпуклый конус излучений, содержащий вместе с любыми излучениями все их выпуклые комбинации (смеси) Поэтому векторы в образуют выпуклый конус , а векторы .

Если то и их аддитивная смесь . Для нее

. (1)

Отсюда следует

Лемма 1. Яркость f_e и цвет j _e любой аддитивной смеси e (Ч) излучений e₁ (Ч),...,e_m (Ч) , m=1,2,... определяются яркостями и цветами слагаемых .

Подчеркнем, что равенство , означающее факт совпадения яркости и цвета излучений e (Ч) и , как правило, содержит сравнительно небольшую информацию об их относительном спектральном составе. Однако замена e (Ч) на в любой аддитивной смеси излучений не изменит ни цвета, ни яркости последней.

Далее предполагается, что вектор w (Ч) таков, что в E можно указать базовые излучения , для которых векторы , j =1,...,n , линейно независимы. Поскольку цвет таких излучений непременно отличен от черного, их яркости будем считать единичными , , j =1,...,n . В таком случае излучение характеризуется лишь цветом , j =1,...,n .

Для всякого излучения e (Ч) можно записать разложение

, (1*)

в котором - координаты в базисе ,

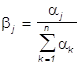или, в виде выходных сигналов детекторов излучения, - , где , , - выходной сигнал i- го детектора, отвечающий j- ому излучению e_j (Ч), i , j =1,...,n . Матрица - стохастическая, поскольку ее матричные элементы как яркости базовых излучений неотрицательны и , j =1,...,n. При этом яркость и вектор цвета , , j =1,...,n , (конец которого лежит в П) определяются координатами a _j и цветами излучений , j =1,...,n , и не зависят непосредственно от спектрального состава излучения e (Ч).

В ряде случаев белое излучение естественно определять исходя из базовых излучений, а не из выходных сигналов детекторов, считая белым всякое излучение, которому в (1*) отвечают равные координаты: .

Заметим, что слагаемые в (1*), у которых a_j <0, [3] физически интерпретируются как соответствующие излучениям, "помещенным" в левую часть равенства (1*) с коэффициентами -a_j >0: . В такой форме равенство (1*) представляет “баланс излучений”.

Определим в скалярное произведение и векторы , биортогонально сопряженные с : , i ,j =1,...,n .

Лемма 2. В разложении (1*) , j=1,...,n , . Яркость , где , причем вектор y ортогонален гиперплоскости П, так как , i,j=1,...,n.

Что касается скалярного проиведения , то его естественно определять так, чтобы выходные сигналы детекторов были координатами f _e в некотором ортонормированном базисе . В этом базисе конус . Заметим, что для любых векторов и, тем более, для , [4] .

Пусть Х - поле зрения, например, ограниченная область на плоскости R₂ , или на сетке , спектральная чувствительность j -го детектора излучения, расположенного в точке ; - излучение, попадающее в точку . Изображением назовем векторнозначную функцию

(2**)

Точнее, пусть Х - поле зрения, (Х , С , m) - измеримое пространство Х с мерой m, C - s-алгебра подмножеств X . Цветное (спектрозональное) изображение определим равенством

--> ЧИТАТЬ ПОЛНОСТЬЮ <--