Реферат: Наближене обчислення визначених інтегралів, що не беруться через елементарні функції /Укр./

Це так звана формула трапецій.

Можно показати, що при зростанні до нескінченності похибка формули прямокутників і формули трапецій нескінченно зменьшується. Таким чином, при достатньо великому обидві ці формули відтворюють шукане значення з довільним рівнем точності.

Параболічне інтерполювання.

Для наближеного обчислення інтеграла можно спробувати замінити функцію «близьким» до неї многочленом

(3)

і покласти

Можно сказати, що тут – при обрахуванні площі – дана «крива» замінюється на «параболу - го порядку» (3), в зв'язку з чим цем процес отримав назву параболічного интерполювання.

Сам вибір інтерполюючуго многочлена частіше всього виконують наступним чином. У проміжку беруть значень незалежної змінної і підбирають многочлен так, щоб при усіх взятих значеннях його значення співпадало зі значенням функції . Цією умовою, як ми знаємо, многочлен визначається однозначно, і його вираз даеться інтерполяціонною формулою Лагранжа:

При інтерполюванні виходить лінійний, відносно значень вираз, коефіцієнти якого вже не залежать від цих значень. Вирахувавши коефіціенти раз і назавжди, можно їх використовувати для будь-якої функції в даному проміжку .

В найпростішому випадку, при , функція просто замінюється сталою , де – будь-яка точка у проміжку , скажемо, середня: . Тоді наближено

(4)

Геометрично – площа криволінійної фігури замінюється тут площадью прямокутника з висотою, яка рівна середній її ординаті.

При функція замінюється лінійною функцією , яка має однакові з нею значення при и . Якщо взяти , , то

(5)

і, як легко обчислити,

Таким чином, тут ми наближено вважаємо

На цей раз площа криволінійної фігури замінюється площею трапеції: замість кривої береться хорда, яка зполучає її кінці.

Менш тривіальний результат отримаємо взявши . Якщо покласти , , , то інтерполяційний многочлен буде мати вигляд

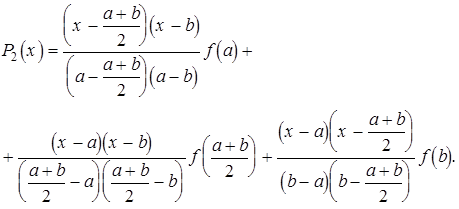(7)

За допомогою легкого обчислення вираховуємо

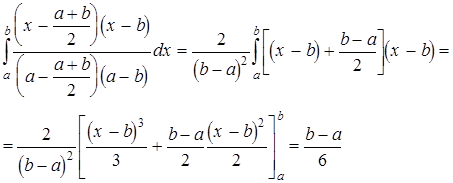
і, аналогічно

,

.

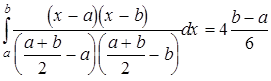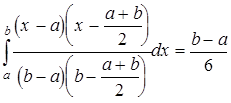Таким чином, приходимо до наближеної формули

.
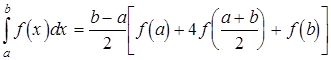