Реферат: Наближене обчислення визначених інтегралів, що не беруться через елементарні функції /Укр./

де міститься між точками и . По відомій властивості неперервної функції, знайдеться в така точка , що , і остаточно

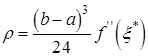. (12)

Якщо зараз розділити проміжок на рівних частин, то для кожного часткового проміжку будемо мати точную формулу

.

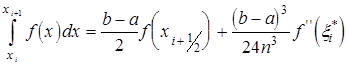
Додавнши ці равенства (при ) почленно отримаємо при звичайних скорочених позначеннях

,

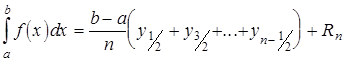де вираз

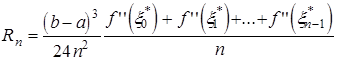
і є залишковий член формули прямокутників (1). Так як вираз

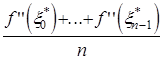
також знаходиться між і , то і він представляє одне із значень функції .

Тому остаточно маємо

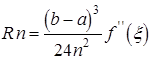
(13).

При зростанні цей додатковий член спадає приблизно як .[1]

Залишковий член формули трапеції.

Займемось тепер формулою (6) при попередніх здогатках відносно функції . Скориставшись інтерполяційною формулою Лагранжа із залишковим членом можемо написати

.

Інтегруя цю формули від до , знайдемо

,

.

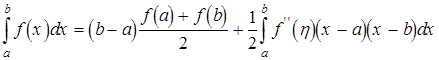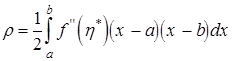Розмірковуючи, як і вище, і користуючись тим, що другий множник підінтегральної функції і тут не змінює знака, знайдемо

.

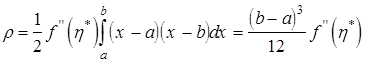
Нарешті, для випадку ділення проміжку на рівних частин

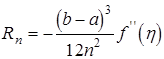
(14).

Таким є залишковий член формули трапецій (2). При зростанні він також зменьшуеться приблизно як . Ми бачемо, що застосування формули трапецій приводить до похибки того ж порядку, що і для формули прямокутників.

Залишковий член формули Сімпсона.

Звернемося, нарешті до формули (8). Можно було б, аналогічно тому, як це було зроблено тількі що, знов скористатись формулою Лагранжа з залишковим членом і покласти

(15).