Реферат: Начала систематического курса стереометрии в средней школе

Пусть SABC тетраэдр. MKP- середины ребер SA, SB, SC

Как располагаются прямые MK, KP, MP относительно ABC?

MK -средняя линия DASB => MK //AB => MK//ABC. Аналогично для др. прямых.

2. Методика изучения перпендикулярности прямых и плоскостей. Методическая схема изучения признака перпендикулярности прямой и плоскости

Содержание: определения: перпендикулярных прямых, перпендикулярных прямой и плоскости, перпендикуляра к плоскости, расстояние от точки до плоскости, наклонной, прямоугольной проекции наклонной, перпендикулярных плоскостей, теоремы о перпендикулярных прямых, признак перпендикулярности прямой и плоскости, теорем о связи между параллельностью и перпендикулярностью прямых и плоскостей в пространстве, теорема о трех перпендикулярах, теорема о перпендикулярных плоскостях.

Т.к. в учебнике Погорелова не вводится понятие о перпендикулярных скрещивающихся прямых то: пряма а , пересекающая плоскость a , называетсяперпендикулярной к плоскости a , если она перпендикулярнак любой прямой в плоскостиa , проходящей через точку пересечения прямой а с плоскостьюa .

Определения, приведенные в этой теме, относятся к генетическим (конструктивным), поэтому при их изучении используют методическую схему, определенную в “2” для параллельного проектирования. Согласно определения к плоскости проводим прямую, кот. пересекает ее в некоторой точке А. В этой плоскости найдется прямая, проходящая через точку пересечения.

Если эта прямая перпендикулярнакданной прямой, то ее называют перпендикулярной к плоскости . По рисунку куба попросить учащихся обозначить ребра куба, перпендикулярные к плоскостям AA₁ BB₁ , ABCD, D₁ C₁ CD, и назвать плоскости, которым перпендикулярны ребра C₁ D₁ , A₁ D₁ , BC.

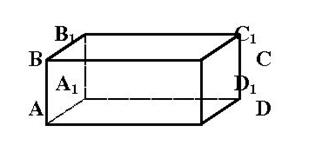
Признак перпендикулярности :

Если прямая, пересекающая плоскость, перпендикулярна к двум прямым в этой плоскости, то она перпендикулярна к плоскости.

Сформулировать эту теорему учащиеся смогут сами, используя приведенную выше задачу (например, ребро А₁ D₁ перпендикулярнок плоскости DD₁ C₁ => А₁ D₁ ^DD₁ и А₁ D₁ ^D₁ С₁ т.е. двум прямым лежащим в этой плоскости).

Методическая схема изучения признака перпендикулярности прямой и плоскости

1) подвести учащихся к признаку, сформулировать его;

2) выполнить рисунок, краткую запись теоремы;

3) сообщать общую идею доказательства теоремы;

4) выполнить доп. построения;

5) сообщать идею доказательства теоремы в более конкретной форме ;

6) привести план доказательства;

7) изложить доказательство ;

8) закрепить доказательство по частям;

9) воспроизведения доказательства полностью;

Для того чтобы подвести учащихся к теореме можно воспользоваться и др. моделью, состоящей из листа картона и нескольких спиц. С ее помощью показать, что если прямая перпендикулярнатолько к одной прямой, расположенной в плоскости a , то этого не достаточно, чтобы прямая а была перпендикулярнакплоскости a .

В учебнике дано слово “пересекающиеся” прямые. Здесь приведено традиционное доказательство, основанное на применении признаков равенства треугольников. Одно из первых доп. построений- проведение через точку А произвольной прямой Х, что необходимо для того чтобы доказать справедливость определения прямой, пересекающей плоскость, этой плоскости. Вторая часть доп. построений: AА₁ =AА₂ , произвольная прямая СВ, пересекающая прямые b, х, с. А₁ С, А₁ Х, А₁ В, А₂ С, А₂ Х, А₂ В - для образования треугольников, равенство которых будет доказано.

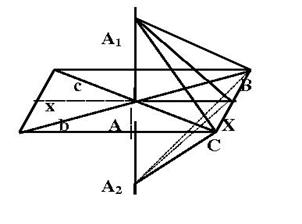
План доказательства:

DА1 СА2	А1 С= А2 С
DА1 ВА2	А1 В= А2 В
DА1 ВС, А2 ВС	DА1 ВС=DА2 ВС=> ÐА1 ВХ= ÐА2 ВХ
DА1 ВХ, А2 ВХ	DА1 ВХ=DА2 ВХ=> А1 Х= А2 Х
DА1 ХА2	х ^ а

При наличии подробного плана доказательства краткую запись делать не целесообразно. Оставшаяся часть проводится устно.

Пункт 1 плана можно осуществить, направляя учащихся вопросами типа: Какую фигуру надо рассмотреть? Какое ее свойство нужно установить?

После того как доказано, что для DА₁ СA₂ выполняется равенство А₁ С=A₂ С?, Почему А₁ С=А₂ С? Почему А₁ В=А₂ В? Почему DА₂ ВС=DА₂ ВС? и т. п.