Реферат: Наукове обґрунтування та розробка моделі завантаження лікувальних закладів охорони здоров’я пацієнтами
де: ![]() – кількість вузлів обслуговування.
– кількість вузлів обслуговування.
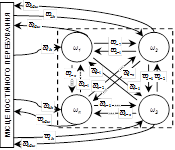 ???. 4. ?????????? ????????????? ????? ???????? ????????? ?????? (?????) ??????? ????????? ?????????????? ??? ??????? ????? ???????????? ????? ???????? ???? ??????? ?? ??????? ?????
???. 4. ?????????? ????????????? ????? ???????? ????????? ?????? (?????) ??????? ????????? ?????????????? ??? ??????? ????? ???????????? ????? ???????? ???? ??????? ?? ??????? ?????  ???. 5. ?????????? ????? k -?? ????? ????????? ??????????????
???. 5. ?????????? ????? k -?? ????? ????????? ??????????????
Інтенсивності потоків пацієнтів в СМО (як внутрішніх так і зовнішніх) залежать від часу і вважаються випадковими величинами.
Для зручності комп’ютерної реалізації в математичній моделі використовувався дискретний спосіб завдання часу, позначеного як ![]() ,
, ![]() ,
, ![]() =1 доба, MaxDay – тривалість часу (в добах), протягом якого здійснюється моделювання. Кожний проміжок часу
=1 доба, MaxDay – тривалість часу (в добах), протягом якого здійснюється моделювання. Кожний проміжок часу ![]() може бути розділений на Step дискретних частин і, таким чином, може розглядатися як час
може бути розділений на Step дискретних частин і, таким чином, може розглядатися як час ![]() ,
, ![]() ,
, ![]() , де Step – так званий крок моделювання, котрий є цілим позитивним числом, частка від ділення на яке одиниці фактично означає частку проміжку часу
, де Step – так званий крок моделювання, котрий є цілим позитивним числом, частка від ділення на яке одиниці фактично означає частку проміжку часу ![]() .
.
![]() , (2)
, (2)
де: ![]() – інтенсивність нестаціонарного адитивного потоку пацієнтів j -ої категорії в момент часу
– інтенсивність нестаціонарного адитивного потоку пацієнтів j -ої категорії в момент часу ![]() ;
;![]() – момент дискретного часу
– момент дискретного часу ![]() ,
, ![]() ;
; ![]() – кількість категорій пацієнтів.
– кількість категорій пацієнтів.
Потік ![]() кожного вузла являє собою потік декількох категорій пацієнтів, що спрямовуються на вузол зовні, кожна категорія пацієнтів в моделі пересувається по унікальній послідовності вузлів обслуговування.
кожного вузла являє собою потік декількох категорій пацієнтів, що спрямовуються на вузол зовні, кожна категорія пацієнтів в моделі пересувається по унікальній послідовності вузлів обслуговування.
В свою чергу вхідний потік пацієнтів j -ої категорії в момент часу ![]() до системи може бути представлений наступним чином:
до системи може бути представлений наступним чином:
![]() , (3)
, (3)
де: ![]() – частка пацієнтів j -ої категорії від загальної кількості осіб з w -м захворюванням або ураженням
– частка пацієнтів j -ої категорії від загальної кількості осіб з w -м захворюванням або ураженням
![]() – коефіцієнт втрат за окремим видом ураження або коефіцієнт захворюваності, що відповідає моменту часу
– коефіцієнт втрат за окремим видом ураження або коефіцієнт захворюваності, що відповідає моменту часу ![]() ,
, ![]() ;
;
![]() – початкова чисельність в момент часу
– початкова чисельність в момент часу ![]() g -ї групи осіб (військова частина, угруповання військ, контингент населення та ін.), медичне забезпечення яких моделюється;
g -ї групи осіб (військова частина, угруповання військ, контингент населення та ін.), медичне забезпечення яких моделюється;
![]() – кількість факторів ураження (видів зброї) та різновидів захворювань на мирний час.
– кількість факторів ураження (видів зброї) та різновидів захворювань на мирний час.
З формули (3) виходить, що однорідні за своїми медичними характеристиками пацієнти, що належать до різних груп осіб, вважаються різними категоріями.
Вихідний потік пацієнтів з системи є нестаціонарним і являє собою суму усіх потоків ![]() . Його інтенсивність у момент часу
. Його інтенсивність у момент часу ![]() (
(![]() ) позначимо як
) позначимо як ![]() :
:
![]() , (4)
, (4)
де: ![]() – інтенсивність вихідного потоку пацієнтів j -ї категорії з k -го вузла в момент часу
– інтенсивність вихідного потоку пацієнтів j -ї категорії з k -го вузла в момент часу ![]() ;
;
![]() – кількість категорій пацієнтів, що спрямовуються на k -й вузол.
– кількість категорій пацієнтів, що спрямовуються на k -й вузол.
Вихідний потік пацієнтів ![]() j -ої категорії з k -го вузла являє собою суму елементарних потоків виписки пацієнтів, що надходили в усі попередні моменти часу
j -ої категорії з k -го вузла являє собою суму елементарних потоків виписки пацієнтів, що надходили в усі попередні моменти часу ![]() :
:
![]() , (5)
, (5)
![]() , (6)
, (6)
де: ![]() – кількість пацієнтів j -ої категорії, що надійшла на лікування у k -му вузлі в момент часу q (надходять з черги
– кількість пацієнтів j -ої категорії, що надійшла на лікування у k -му вузлі в момент часу q (надходять з черги ![]() );
);
NFlowOut – кількість можливих станів пацієнтів (можливими станами є повне одужання, смерть та ін.);
![]() – імовірність виписки пацієнтів j -ої категорії з k -го вузла у стан f в момент часу
– імовірність виписки пацієнтів j -ої категорії з k -го вузла у стан f в момент часу ![]() ;
;
![]() – імовірність виписки пацієнтів j -ої категорії з k -го вузла у стан f в момент часу
– імовірність виписки пацієнтів j -ої категорії з k -го вузла у стан f в момент часу ![]() , який відповідає моменту часу
, який відповідає моменту часу ![]() ;
; ![]() , де
, де ![]() – максимальний час лікування пацієнтів j -ої категорії у k -му вузлі (у добах);
– максимальний час лікування пацієнтів j -ої категорії у k -му вузлі (у добах);
![]() ,
, ![]() 1 ; (7)
1 ; (7)
b – індекс, що визначає вид моделі виписки, b = 0 для загальної нестаціонарної моделі, b = 1…7 для диференційованої нестаціонарної моделі (цими числами кодуються дні тижня, індекс b обчислюється відповідно до реальної дати надходження пацієнтів спеціальною функцією Delphi).
Інші формули математичної моделі описують переміщення пацієнтів з черги x k на медичне обслуговування в чергу ![]() на транспортування з вузла та в місце остаточного лікування, а також вплив факторів ризику на транспортні ресурси вузлів обслуговування та ресурси робочого часу на надання медичної допомоги.
на транспортування з вузла та в місце остаточного лікування, а також вплив факторів ризику на транспортні ресурси вузлів обслуговування та ресурси робочого часу на надання медичної допомоги.
Перевагою запропонованої математичної моделі є те, що вона дозволяє представляти потоки надходження та виписки пацієнтів як стаціонарні, так і складні нестаціонарні процеси. При цьому в моделі (формула 6) можливе представлення ймовірностей виписки (![]() ) у вигляді аналітичних функцій або дискретного набору ймовірностей.
) у вигляді аналітичних функцій або дискретного набору ймовірностей.
Розроблена математична модель була реалізована в комп’ютерних програмах “Модель системи надання медичної допомоги та етапного лікування” (“Model”) та “Модель закладу охорони здоров’я” (“Hospital”). Відповідно були розроблені алгоритми роботи та реляційна модель бази даних програмного забезпечення.