Реферат: Необхідні умови оптимальності. Принцип максимуму Понтрягіна
4. Припустимо, 
– оптимальна траєкторія, що відповідає керуванню 
, 
, 
. Розглянемо довільний відрізок 
, і позначимо 
, 
. За таких умов інтеграл 
на керуванні набуває найменшого значення серед всіх припустимих керувань 
, що переводять систему зі стану 
в стан 
.
3 Принцип максимуму Понтрягіна
Розглянемо задачу оптимального керування (1), (3)–(5):
, 
, 
,
,
, 
, 
, 
,
де 
, 
– функції, неперервні за сукупністю всіх змінних і неперервно-диференційовані по змінних 
.
Перейдемо до 
-вимірного простору, елементами якого є вектори
,
де 
– фазовий вектор задачі, а 
– деяка функція, що задовольняє співвідношенню
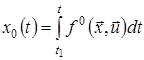.(6)
З останньої формули випливає, що функція 
є розв’язком рівняння
.
Приєднавши останнє рівняння до системи (1), дістанемо нову систему
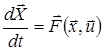,(7)
де 
;
.
Підкреслимо, що праві частини рівнянь системи (7) не залежать від 
. З формули (6) випливає, що
, 
.
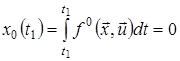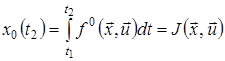Таким чином, початкову задачу зведено до задачі вибору припустимого керування , яке здійснює перехід точки 
в -вимірному просторі зі стану 
у найближчу точку 
на прямій, що паралельна осі 
, і проходить через точку 
(рис. 3). Пошук оптимального керування тепер полягає в мінімізації величини 
. Дійсно,
.
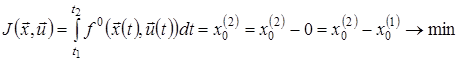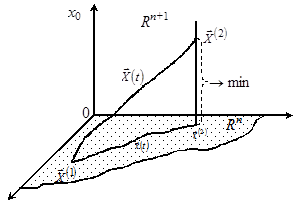
Рисунок 3
Складемо допоміжну систему
, 
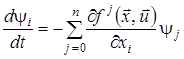,(8)
відносно невідомих функцій 
. Ця система називається спряженою системою до системи (7), а змінні – спряженими змінними.
Якщо 
– припустимий процес, то відповідна цьому процесу система (8) є лінійною однорідною системою диференціальних рівнянь із відомими кусково-неперервними коефіцієнтами. Відомо, що за будь-яких початкових умов ця система має єдиний розв’язок.
Оскільки 
, 
, не залежать від , то
,
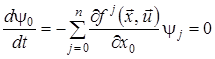