Реферат: Необхідні умови оптимальності. Принцип максимуму Понтрягіна

Розглянемо функцію

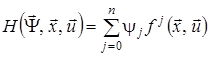,(9)

що називається функцією Понтрягіна, де – вектор спряжених змінних. Точну верхню грань значень цієї функції по змінній при фіксованих і позначимо через

.

Має місце наступна теорема.

Теорема 1 (принцип максимуму). Якщо керування , і відповідна йому фазова траєкторія оптимальні, то існує така ненульова вектор-функція , що відповідає функціям і (тобто задовольняє спряженій системі (8) з функціями й ), що:

1. Функція від змінної набуває максимуму в точці для будь-якого :

: .

У кінцевий момент часу має місце співвідношення , .

Умови теореми 1 дозволяють серед усіх траєкторій, що проходять через дві задані точки й , виділити окремі траєкторії, серед яких перебуває і оптимальна траєкторія, якщо вона існує. Ці умови є необхідними, але не достатніми. Потрібна подальша перевірка знайдених траєкторій на оптимальність. Тільки в найпростішому випадку, коли знайдено лише одну траєкторію, а з деяких міркувань відомо, що оптимальний розв’язок існує, можна стверджувати, що знайдена траєкторія і є оптимальною.

Якщо принципу максимуму задовольняють кілька траєкторій, то для виявлення серед них оптимальної треба застосовувати додаткові умови. Іноді вдається відокремити сторонні траєкторії, порівнюючи значення цільового функціонала. Але оптимальна траєкторія може бути не єдиною, а відкинуті траєкторії, не будучи оптимальними, можуть виявитися локально оптимальними.

Продиференціюємо функцію Понтрягіна (9) за змінними і :

, ,

, .

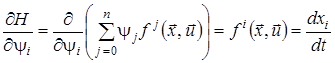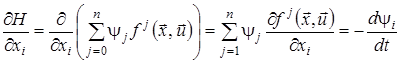Тепер співвідношення (7) і (8) можна переписати у вигляді гамільтонової системи:

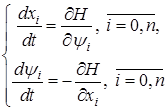.(10)

Якщо , , задовольняють системі (10) і умові 1 теореми 1, то функції і змінного є сталими. Умова 2 теореми 1, таким чином, має місце в будь-який момент часу .

4 Принцип максимуму для задачі оптимальної швидкодії

Окремим випадком критерію (5) є критерій

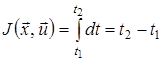,(11)

який називається критерієм оптимальної швидкодії, а відповідна йому задача – задачею оптимальної швидкодії. Оскільки у формулі (11) , то функція Понтрягіна для задачі оптимальної швидкодії матиме вигляд:

,

де .

Оскільки перший доданок не залежить від , то максимум функції по реалізується одночасно з максимумом функції

,

де . Тому далі розглядатимемо нову гамільтонову систему, відкинувши перші рівняння системи (10), що відповідають :

.(12)

Позначимо

.