Реферат: Неопределенные бинарные квадратичные формы

Доказательство. Пусть и — канонические разложения чисел и , и пусть

, ,…, — все простые делители наибольшего общего делителя чисел и . Тогда ясно, что

. (1)

Но так как справедливо неравенство

, (2)

то неравенство (1) с учетом (2) и предложения 2 перейдет в следующие соотношения:

Предложение 3 доказано.

Предложение 4. Для имеет место неравенство

,

где —произвольное положительное число, —постоянная, зависящая только от .

Доказательство. Мы следуем рассуждениям в [4,5] (доказательство имеется также в [3]). Пусть — каноническое разложение числа . Тогда имеем:

Рассмотрим отношение , в случаях и .

Если , то , так как .

Если , то считая , получим:

Поэтому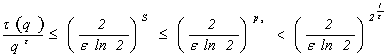

Следовательно, полагая 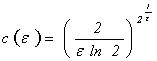, получим неравенство

Предложение 4 доказано.

Следующее предложение характеризует среднее значение в нужной для нас форме

Предложение 5. Для имеет место следующая оценка сверху:

,

где — постоянная

Доказательство. Имеем: