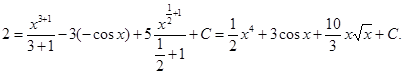Реферат: Неопределенный интеграл

Теорема 1.Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов:

(1)

Из доказательства найдем производные от левой и правой частей этого равенства. На основании равенства (4) пункта №1 находим

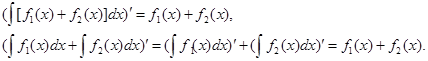
Таким образом, производные от левой и правой частей равенства (1) равны между собой, т. е. производная от любой первообразной, стоящая в левой части, равняется производной от любой функции, стоящей в правой части равенства. Следовательно по теореме из пункта №1 любая функция, стоящая в левой части равенства (1), отличается от любой функции, стоящей в правой части равенства(1), на постоянное слагаемое. В этом смысле и нужно понимать равенство (1).

Теорема 2. Постоянный множитель можно выносить за знак интеграла, т. е. если a=const, то

(2)

Для доказательства равенства (2) найдем производные от левой и правой его частей:

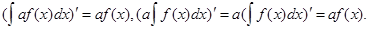
Производные от правой и левой частей равны, следовательно, как и в равенстве (1), разность двух любых функций, стоящих слева и справа, есть постоянная. В этом смысле и следует понимать равенство (2).

При вычислении неопределенных интегралов бывает полезно иметь в виду следующие правила.

1).Если

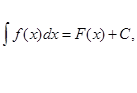
то

(3)

Действительно, дифференцируя левую и правую части равенства (3) получим

Производные от правой и левой частей равны, что и требовалось доказать.

2). Если

то

(4)

3. Если

то

. (5)

Равенства (4) и (5) доказываются дифференцированием правой и левой частей равенств.

Пример 1.

=