Реферат: Неопределенный интеграл

=

=

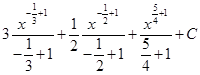Пример 3.

.

Пример 4.

Пример 5.

4)Интегрирование методом замены переменой или способом подстановки

Пусть требуется найти интеграл , причем непосредственно подобрать первообразную для f(x) мы не сможем , но нам известно, что она существует.

Сделаем замену переменной в подынтегральном выражении, положив

x=φ(t), (1)

где φ(t)-непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда dx= φ′(t)dt;докажем, что в этом случае имеет место следующее равенство:

(2)

Здесь подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х на основании равенства (1).

Для того чтобы установить, что выражения, стоящие справа и слева, одинаковы в указанном выше смысле, нужно доказать, что их производные по х равны между собой . Находим производную от левой части : Правую часть равенства (2) будем дифференцировать по х как сложную функцию, где t-промежуточный аргумент. Зависимость t от х выражается равенством (1), при этом и по правилу дифференцирования обратной функции .

Таким образом, имеем

Следовательно, производные от х от право й и левой частей равенства (2) равны, что и требовалось доказать.

Функцию следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства (2).

Замечание. При интегрировании иногда целесообразнее подбирать замену переменной не в виде , а в виде Проиллюстрируем это на примере. Пусть нужно вычислить интеграл, имеющий вид

.

Здесь удобно положить

,

тогда

.

Приведем несколько примеров на интегрирование с помощью замены переменных.

Пример 1.

Сделаем подстановку t=sin x; тогда dt= cosx dx и, следовательно,