Реферат: Неравенства

2) Парабола пересекает ось 0х (т. е. уравнение ах² + bх + с = 0 имеет два различных корня). То есть, если а<0 то решением неравенства является множество [x1;x2].

y = ах² +bх + с a>0 D>0 y = ах² +bх + с a <0 D >0,

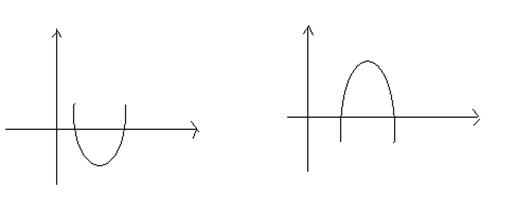
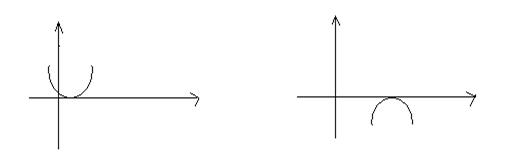
Парабола имеет вершину на оси 0х (т. е. уравнение ах² + х + с = 0 имеет один корень, так называемый двукратный корень) То есть, если d=0, то при a>0 решением неравенства служит вся числовая прямая, а при a<0 единственная точка х1, являющаяся единственным корнем квадратного трехчлена ах² + х + с

y = ах² +bх + с a>0 D = 0 y = ах² +bх + с a <0 D =0,

3) Если d<0 то график квадратного трехчлена f(x) = ах² +bх + с не пересекает ось Ох и лежит выше этой оси при a>0 и ниже ее при a<0 В первом случае множество решений неравенства есть вся числовая прямая, а во втором оно является пустым.

4)

y = ах² +bх + с a>0 D < 0 y = ах² +bх + с a <0 D< 0,

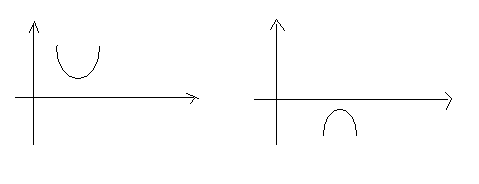
4) Решить неравенство графическим способом

1) 3х² -4х ;

3х² -4х.

1. Пусть f(x) = 3х² -4х - 7 тогда найдем такие х при которых f(x) ;

2. Найдем нули функции.

3х² -4х-7=0,

D=100,

Х=-1 Х=7\3.

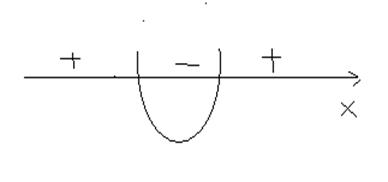
f(x) при х .

Ответ f(x) при х .

2) х² >-4x-5;

x² +4x +5>0;

Пусть f(x)=х² +4х +5 тогда Найдем такие х при которых f(x)>0,

X² +4x+5=0,

D=-4 Нет нулей.

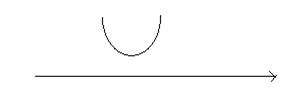
Ответ .

4. Системы неравенств. Неравенства и системы неравенств с двумя переменными

1) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств.