Реферат: Неравенства
3) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств. Пусть, например, задана система неравенств:
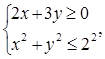 .
.
Для первого неравенства множество решений есть круг радиусом 2 и с центром в начале координат, а для второго- полуплоскость, расположенная над прямой 2х+3у=0. Множеством решений данной системы служит пересечение указанных множеств, т.е. полукруг.
4) Пример. Решить систему неравенств:
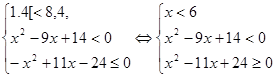
Решением 1-го неравенства служит множество ![]() , 2-го множество (2;7) и третьего - множество
, 2-го множество (2;7) и третьего - множество ![]() .
.
Пересечением указанных множеств является промежуток(2;3], который и есть множество решений системы неравенств.
5. Решение рациональных неравенств методом интервалов
В основе метода интервалов лежит следующее свойство двучлена (х-а ): точка х=α делит числовую ось на две части — справа от точки α двучлен (х‑α)>0 , а слева от точки α (х-α)<0 .
Пусть требуется решить неравенство (x-α1 )(x-α2 )...(x-αn )>0 , где α1 , α2 ...αn-1 , αn — фиксированные числа, среди которых нет равных, причем такие, что α1 < α2 <...< αn-1 < αn . Для решения неравенства (x-α1 )(x-α2 )...(x‑αn )>0 методом интервалов поступают следующим образом: на числовую ось наносят числа α1 , α2 ...αn-1 , αn ; в промежутке справа от наибольшего из них, т.е. числа αn , ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем — знак «плюс», затем знак «минус» и т.д. Тогда множество всех решений неравенства (x-α1 )(x‑α2 )...(x-αn )>0 будет объединение всех промежутков, в которых поставлен знак «плюс», а множество решений неравенства (x-α1 )(x-α2 )...(x‑αn )<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Решение рациональных неравенств (т.е неравенств вида ![]() P(x) Q(x) где – многочлены) основано на следующем свойстве непрерывной функции: если непрерывная функция обращается в нуль в точках х1 и х2 (х1;х2) и между этими точками не имеет других корней, то в промежутках(х1;х2) функция сохраняет свой знак.
P(x) Q(x) где – многочлены) основано на следующем свойстве непрерывной функции: если непрерывная функция обращается в нуль в точках х1 и х2 (х1;х2) и между этими точками не имеет других корней, то в промежутках(х1;х2) функция сохраняет свой знак.
Поэтому для нахождения промежутков знакопостоянства функции y=f(x) на числовой прямой отмечают все точки, в которых функция f(x) обращается в нуль или терпит разрыв. Эти точки разбивают числовую прямую на несколько промежутков, внутри каждого из которых функция f(x) непрерывна и не обращается в нуль, т.е. сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой либо точке рассматриваемого промежутка числовой прямой.
2) Для определения интервалов знакопостоянства рациональной функции, т.е. Для решения рационального неравенства, отмечаем на числовой прямой корни числителя и корни знаменателя, которые как и являются корнями и точками разрыва рациональной функции.
Решение неравенств методом интервалов
3. ![]() < 20.
< 20.
Решение . Область допустимых значений определяется системой неравенств:
![]() .
.
Для функции f(x) = ![]() – 20. Находим f(x) :
– 20. Находим f(x) :
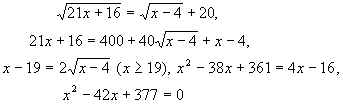
откуда x = 29 и x = 13.
f (30) =![]() – 20 = 0,3 > 0,
– 20 = 0,3 > 0,
f (5) =![]() – 1 – 20 = – 10 < 0.
– 1 – 20 = – 10 < 0.
Ответ: [4; 29).
х2 +х-2![]()
Пусть f(x)=х2 +х-2 тогда найдем такие х при которых f(x)<0.
Найдем нули х=1, х=-2.
![]()
х3 -4х<0
x(x2 -4)<0
x(x-2)(x+2)<0