Реферат: Нормальный закон распределения
СОДЕРЖАНИЕ
1. ВВЕДЕНИЕ 6
1. ОСНОВНЫЕ ПАРАМЕТРЫ И ОПРЕДЕЛЕНИЯ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ 8
1.1. Нормальное распределение 8
1.2. Статистическая гипотеза 8
1.3. Ошибки первого и второго рода. Уровень значимости 9
1.4. Степень свободы параметра 10
1.5. Критическая область. Область принятия гипотезы. 10
1.6. Критерий Стьюдента 11
1.7. Критерий Фишера 13
1.8. Критерий Кохрэна 15
1.9. Критерий Пирсона 15
2. ХАРАКТЕРИСТИКА ПАКЕТА EXCELL 19
3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ 21
4. 4. ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ДАННЫХ В ВЫБОРКЕ 24
4. РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ О НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ДАННЫХ В ВЫБОРКЕ 26
ЗАКЛЮЧЕНИЕ 28
ЛИТЕРАТУРА 29
ВВЕДЕНИЕ
Нормальное (гауссовское) распределение занимает центральное место в теории и практике вероятностно-статистических исследований. В качестве непрерывной аппроксимации к биномиальному распределению его впервые рассматривал А.Муавр в 1733 г. Через некоторое время нормальное распределение снова открыли и изучили К.Гаусс (1809 г.) и -П.Лаплас, которые пришли к нормальной функции в связи с работой по теории ошибок наблюдений.
Цельих объяснения механизма формирования нормально распределенных случайных величин заключается в следующем. Постулируется, что значения исследуемой непрерывной случайной величины формируются под воздействием очень большого числа независимых случайных факторов, причем сила воздействия каждого отдельного фактора мала и не может превалировать среди остальных, а характер воздействия - аддитивный (т.е. при воздействии случайного фактора F на величину а получается величина ___________, где случайная "добавка" ______ мала и равновероятна по знаку).
Во многих случайных величинах, изучаемых в технике и других областях, естественно видеть суммарный аддитивный эффект большого числа независимых причин. Но центральное место нормального закона не следует объяснять его универсальной приложимостью.
В этом смысле нормальный закон - один из многих типов распределения, имеющихся в природе, однако с относительно большим удельным весом практической приложимости.
Однако полнота теоретических исследований, относящихся к нормальному закону, а также сравнительно простые математические свойства делают его наиболее привлекательным и удобным в применении. Даже в случае отклонения исследуемых экспериментальных данных от нормального закона существует, по крайней мере, два пути его целесообразной эксплуатации: во-первых, использовать нормальный закон в качестве первого приближения (при атом нередко оказывается, что подобное допущение дает достаточно точные с точки зрения конкретных целей исследования результаты); во-вторых. подобрать такое преобразование исследуемой случайной величины, которое видоизменяет исходный "не нормальные" закон распределения, превращая его в нормальный.
Удобно для статистических приложений и свойство "самовоспроизводимости" нормального закона, заключающееся в том, что сумма любого числа нормально распределенных случайных величин тоже подчиняется нормальному закону распределения. Кроме того, с помощью закона нормального распределения выведен целый ряд других важных распределений, построены различные статистические критерии
1. ОСНОВНЫЕ ПАРАМЕТРЫ И ОПРЕДЕЛЕНИЯ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ
1.1. Нормальное распределение
В приложениях статистики чаще всего используется нормальное (гауссовское) распределение. Непрерывная случайная величина Х называется распределенной по нормальному закону с параметрами ______, если ее плотность распределения есть
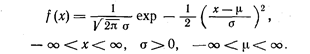
.
1.2. Статистическая гипотеза
Часто необходимо знать закон распределения генеральная совокупности. Если он неизвестен, но есть основания предположить, чтоон имеет определенный вид (назовем его А), выдвигают гипотезу: генеральная совокупность распределена по закону А. Таким образом, в этой гипотезе речь вдет о виде предполагаемого распределения.
Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предположить, то неизвестный параметр Q равен определенному значению Q 0 , выдвигают гипотезу: Q = Q 0 . Таким образом, в этой гипотезе речь идет о предполагаемой величине параметра одного известного распределения.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--