Реферат: О полноте систем упражнений по математическому анализу
Е. А. Меньшикова
Разработкой требований к системам упражнений по математике занимались различные авторы (П.М.Эрдниев, Ю.М.Колягин, Н.А.Сорокин, В.А.Онищук, В.В.Гузеев, А.Ф.Эсаулов и другие). При этом многие из них уделяют значительное внимание требованию полноты. Данная статья анализирует понятие полноты системы упражнений в контексте преподавания математического анализа. При этом мы обосновываем следующие утверждения.
Требования современной дидактики к системам упражнений по той или иной теме математики могут быть обеспечены только такими системами, которые имеют достаточно большой объем и весьма сложную структуру.
Системы упражнений по теме "Экстремум функции", содержащиеся в традиционно используемых задачниках по математическому анализу, не полны в целом ряде отношений.
§1. Принцип полноты
Одним из стандартных требований, предъявляемых к системам упражнений, является требование полноты. Понятие полноты обсуждалось разными авторами, каждый из которых уделяет особое внимание тому или иному аспекту данного понятия.
Так, П.М.Эрдниев изучает данное понятие в рамках своей концепции укрупнения дидактических единиц [10. С.30-35]. Понятие полноты рассматривается в связи с вопросом о наборе упражнений для достижения целостного и прочного усвоения знаний. Говоря об упражнениях, П.М.Эрдниев вводит понятие циклической полноты. Под циклической полнотой понимается такая организация упражнения, когда каждый элемент данного выражения (задачи) последовательно выступает в качестве искомого. П.М.Эрдниев также указывает на необходимость концентрической организации материала, когда в качестве единицы структуры программы выступает цикл, образующий внутренне целостную тему. Например, целесообразно изучать одновременно линейные уравнения, линейные неравенства и тождества, приводящие к линейным уравнениям. Пройдя данный цикл, учащиеся снова возвращаются к уравнению, но уже квадратному. Понятие полноты возникает и в связи с понятийным окружением соответствующих знаний. Согласно П.М.Эрдниеву содержание любого математического понятия или результат математических действий необходимо обогащать, привлекая понятия из других разделов математики. Например, при изучении системы двух линейных уравнений с двумя неизвестными целесообразно давать геометрическую интерпретацию полученного результата. При данном подходе алгебраический результат и его геометрический образ выступают в качестве фона друг для друга. Такое взаимное влияние результатов связано с понятием фоновой наглядности [8. С.203].
В.В.Гузеев рассматривает вопрос о полноте системы упражнений к блоку уроков по той или иной теме. Требование полноты заключается "... в наличии задач на все изучаемые понятия, факты, способы деятельности, включая мотивационные, подводящие под понятие, на аналогию, следствия из фактов и т.д."[4. С.54]
Г.И.Саранцев в своей книге [7] не ставит вопрос о полноте системы упражнений. Однако, рассматривая процесс формирования понятия или организацию работы с теоремой, он указывает на необходимость упражнений для реализации каждого этапа работы. Каждый этап реализуется в процессе выполнения различных действий, следовательно, нужны упражнения на все эти действия. Например, одним из этапов формирования понятия является усвоение его логической структуры. На данном этапе могут быть использованы упражнения на распознавание, на выведение следствий, упражнения, требующие анализа условий, дополнения их таким образом, чтобы из условий вытекала принадлежность объекта понятию [7. С.73]. Таким образом, система упражнений только для формирования понятия должна иметь большой объем и быть хорошо структурированной. Г.И.Саранцев также подчеркивает необходимость формирования обобщенных умений (переформулировка требований задачи, составление промежуточных задач и т.д.) в процессе изучения конкретных понятий, теорем и их совокупностей, поэтому необходимо предусматривать упражнения, позволяющие организовать работу по формированию данных умений.
Ряд авторов рассматривает вопрос о полноте системы упражнений с позиции разнообразия организационных форм работы. Так, А.П.Иванов и Ю.Ф.Фоминых [6] указывают на необходимость наличия баз дидактических заданий по разделам, по темам, по типам; баз контрольных работ, индивидуальных заданий, тематических и итоговых тестовых работ.
А.В.Ястребов [11] рассматривает не отдельные системы упражнений, а задачник по математике в целом. Задачник является средством организации деятельности всех участников процесса обучения. Задачник по стандартному курсу тем лучше, чем более разнообразные виды деятельности могут быть организованы на его основе. Согласно концепции обучения математике как модели научных исследований задачник является средством моделирования различных аспектов научно-исследовательской работы на практических занятиях [11. C.38]. В силу этого задачник должен выполнять ряд специфических функций: 1) отражать современное состояние науки; 2) демонстрировать индуктивный характер математического творчества; 3) давать возможность моделировать информационный обмен, происходящий в науке. Наряду с выполнением данных функций необходимо учитывать тенденции современного образования. А.В.Ястребов указывает следующие тенденции и вытекающие из них требования к задачнику. Во-первых, это дифференциация и индивидуализация обучения. Выделяются три направления дифференциации обучения: 1) базовая - предоставление каждому студенту личного набора стандартных упражнений для выработки прочного навыка их решения; 2) восстановительная - возможность ликвидации пробелов в знаниях студентов, возникших при изучении предыдущих разделов; 3) пропедевтическая - предоставление сильным студентам блоков заданий, способствующих углубленному изучению каких-либо разделов математики или подводящих к решению задач научно-исследовательского характера. Вторая тенденция - профессиональная направленность обучения. Применительно к задачнику для педагогических вузов это означает выдвижение на первый план идеи преемственности обучения в школе и вузе, идеи связи курсов высшей математики с соответствующими школьными предметами, взаимосвязи абстрактных понятий высшей математики со школьными понятиями [11. С.35]. Третья тенденция - это тенденция самостоятельного изучения отдельных вопросов программы в результате решения большой серии специальным образом подобранных упражнений. Для реализации данной тенденции в задачнике целесообразно предусмотреть возможность изучения ряда разделов математики в "задачах".
Рассмотренные точки зрения показывают многообразие трактовок принципа полноты, сложившихся к настоящему времени в методической литературе. Это связано с разнообразием требований, положенных авторами в основу данного понятия. Однако, несмотря на кажущееся разнообразие, данные требования можно разбить на небольшое число групп:
требования, предъявляемые к математическому содержанию упражнений;
требования, вызванные необходимостью учета психологии обучаемых;
требования, предъявляемые к системам упражнений как способу организации учебного процесса.
Детализируем данную типологию, выделив ряд аспектов понятия полноты, которые представим в виде меню:
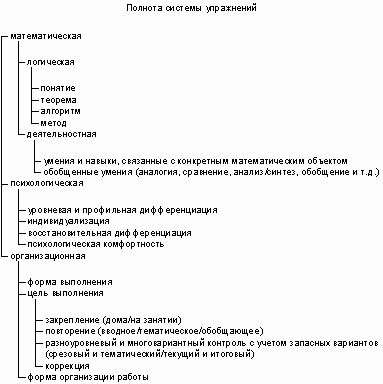
Математическая полнота системы упражнений характеризует степень отражения многообразия математических особенностей изучаемого материала в упражнениях. Говоря о математической полноте системы упражнений, необходимо различать усвоение понятий, теорем, алгоритмов и освоение практических умений, связанных с ними.
Усвоение понятия заключается в усвоении содержания понятия, его объема, существенных связей данного понятия с другими понятиями и фактами. Таким образом, система упражнений для изучения математического понятия должна включать упражнения, касающиеся всех существенных свойств данного понятия (т.е. упражнения, раскрывающие его содержание) и всех его типичных представителей (т.е. упражнения, раскрывающие его объем). Рассмотрим, например, понятие экстремума. Данное понятие изучается не изолированно, а в окружении других математических понятий, поэтому нужно привести примеры функций, обладающих различными свойствами в окрестности экстремальных точек. Так, говоря об экстремумах и монотонности, нужно рассмотреть различные сочетания типов монотонности по разные стороны экстремальной точки. На схеме №1 представлены различные функции, имеющие локальный минимум в точке x0=0. (Здесь дельта-функция ![]() определяется равенством
определяется равенством ![]() ;
; ![]() - функция Дирихле.)
- функция Дирихле.)
Схема №1
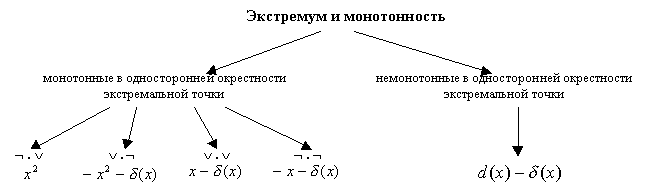
Отступим на время от основной линии нашего изложения и покажем, что рассмотрение примеров может выявить существенные свойства изучаемых понятий. Схема №1 показывает, что монотонность функции в открытой односторонней окрестности точки, рассматриваемая сама по себе, без привлечения дополнительных свойств, не связана с понятием экстремума. Аналогичный вывод мы получим, рассмотрев понятия экстремума и непрерывности (схема №2), экстремума и дифференцируемости (схема №3).
Схема №2
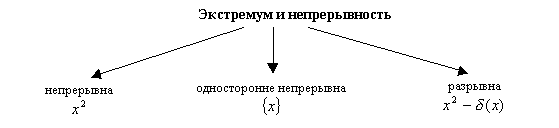
Схема №3
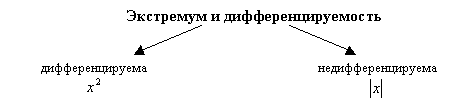
Подобное варьирование несущественных признаков способствует более полному выявлению объема понятия и предупреждает возникновение и упрочение представлений о том, что, например, в точке экстремума функция меняет характер монотонности.
Вернемся к основной линии нашего изложения. В упражнениях должны быть представлены различные способы математических действий с данным понятием: определение принадлежности к объему понятия, дополнение условий таким образом, чтобы объект принадлежал понятию, построение объектов, принадлежащих объему понятия, оперирование данным понятием при решении задач и т.д. Так, среди способов работы с понятием экстремума можно указать следующие:
доказать, что данная точка является точкой экстремума функции (используя определение или достаточное условие существования экстремума);
исследовать функцию на экстремум и, в случае наличия экстремума, установить его характер;
--> ЧИТАТЬ ПОЛНОСТЬЮ <--