Реферат: Об ориентационном взаимодействии спиновых систем

В предыдущей статье [1] при анализе результатов экспериментов по изучению ядерного магнитного резонанса в системе ядерных спинов [2, 3] был сделан вывод о несводимости обнаруженного в экспериментах спин-спинового взаимодействия к теплообмену, а также к электрическому или магнитному мультипольному взаимодействию. Специфика этого взаимодействия, названного нами ориентационным, проявилась в передаче упорядоченной ориентации одной системы ядерных спинов другой и в самопроизвольном установлении при этом единой «средневзвешенной» ориентации различно (в том числе противоположно) направленных спинов. Специфичность этого взаимодействия признается и квантовой механикой, согласно которой главную роль в установлении спин-спинового равновесия играет некоторое особое взаимодействие, названное обменным. Так называют взаимное влияние тождественных частиц, которое обусловлено действием так называемых обменных сил и присутствует даже в случае, если прямым силовыми (электрическим, магнитным) взаимодействием частиц можно пренебречь [4]. Однако обменные силы становятся заметными только тогда, когда среднее расстояние между частицами становится сравнимым с длиной волны де Бройля. Поэтому представляет интерес показать, что ориентационное взаимодействие спиновых объектов имеет место и в макромире.

Ориентационная составляющая потенциальной энергии

Известно, что различные положения тела в пространстве и его различные ориентации в нем с механической точки зрения не эквивалентны [5]. Изучению ориентационной составляющей энергии системы (т.е. той её части, которая зависит от взаимной ориентации её частей) до настоящего времени уделялось недостаточно внимания. Возможно, это было связано с тем, что для решения многих практических задач законы движения тел было удобнее сводить к законам движения отдельных материальных точек, ориентация которых в пространстве уже не имела значения. Это позволяло ограничиться рассмотрением так называемых центральных полей, потенциальная энергия которых U(r) зависела только от расстояния между телами (от радиус-вектора центра их инерции r). Иное дело, когда в качестве объекта исследования выбирается вся совокупность взаимодействующих (взаимно движущихся) тел. Именно к ней как к замкнутой системе и относятся законы сохранения. Рассмотрим, в частности, законы сохранения импульса P и момента импульса L замкнутой механической системы, состоящей из k–х тел (k=1,2,...,К):

(1)

где P_k =m_k v_k ;L_k =r_k ×P_k – импульс k-го тела и момент его импульса; r_k , m_k , v_k – радиус-вектор, масса и скорость центра инерции тела.

Согласно (1), изменение импульса P_k или момента импульса L_k любого из тел замкнутой системы невозможно без равных им по величине и противоположных по знаку изменений импульса или момента импульса всех остальных тел в тот же момент времени. С учетом конечной скорости взаимодействия это означает наличие соответствующих полей сил F_k =dP_k /dt и крутящих моментов M_k =dL_k /dt во всех точках рассматриваемой системы.

Параметры P_k и L_k можно представить в виде произведения их модулей P_k =|P_k | и L_k =|L_k | и единичного вектора e_k , характеризующего их направление, т.е. P_k =Pe_k и L_k =Le_k . Если классифицировать процессы по особым, не сводимым к другим изменениям состояния, которые они вызывают, то следует признать, что производные по времени t от параметров системы P_k и L_k характеризуют, вообще говоря, два различных процесса. Один из них – процесс ускорения соответственно поступательного и вращательного движения e_k (dP_k /dt) и e_k (dL_k /dt), выражающийся в изменении величины импульса P_k или его момента L_k при неизменном их направлении e_k . Другой – процесс переориентации этого движения P_k (de_k /dt) и L_k (de_k /dt), выражающийся в изменении направления векторов P_k и L_k при неизменной величине самого импульса P_k или его момента L_k . Следовательно, изменение направления скорости v_k или момента импульса L_k каждого из тел рассматриваемой системы также с необходимостью сопровождается переориентацией импульса или момента импульса всех других тел данной системы. Силы, порождающие поля F_k и M_k , принципиально отличаются по своей природе. Если, например, ускорение тела осуществляется полем центральных сил F_k , являющихся полярными векторами, то процесс его переориентации (поворота) – центростремительными силами, силами Кориолиса или магнитной составляющей силы Лоренца, являющимися аксиальными векторами. Принято считать, что эти последние силы не совершают никакой работы, поскольку они всегда направлены по нормали к вектору скорости тела v_k . Отсюда якобы следует, что не существует какой-либо формы энергии, соответствующей этим силам. Между тем в замкнутой системе действуют лишь пары таких сил, т.е. крутящие моменты M_k , которые и совершают работу переориентации тел. Действительно, элементарное изменение положения любой материальной точки твердого тела ds можно представить в виде суммы члена dR, характеризующего поступательное движение тела относительно неподвижной системы отсчета, и вектора dφ×r, характеризующего его поворот вокруг мгновенной оси вращения на бесконечно малый угол dφ (где r – радиус-вектор точки в подвижной (сопутствующей) системе координат) [2]:

ds = dR + dφ×r. (2)

Согласно (2), элементарная работа dW_k =F_k ·ds_k какой-либо результирующей силы F_k также складывается из работы смещения тела F_k ·dR_k и работы его поворота F_k ·(dφ_k ×r_k )=M_k ·dφ_k , где M_k =dL_k /dt=r_k ×F_k – крутящий момент, действующий на k-е тело. Таким образом, переориентация тел осуществляется полем моментов M_k и также связана с совершением определенной работы, Это свидетельствует о существовании специфической составляющей потенциальной энергии, которую уместно назвать ориентационной энергией.

Наличие поля крутящих моментов M_k , передающего изменение ориентации одних тел другим, свойственно, вообще говоря, любым упорядоченным формам энергии. Известно, например, что поляризация диэлектриков сопровождается не только разделением в пространстве положительных и отрицательных зарядов (т.е. созданием диполей), но и переориентацией по полю уже имеющихся «жестких» диполей с неизменным плечом [6]. На это расходуется часть работы поляризации dW_е =E·dZ_e , где E – напряженность электрического поля, Z_e – вектор поляризации. Эта часть в соответствии с вышеизложенным определяется выражением dW_е =Z_e E·de и может быть представлена в виде произведения действующего на электрический диполь крутящего момента M_Е на элементарный угол его поворота dφ_е в поле E. Точно так же в процессе намагничивания наряду с изменением плеча магнитных диполей происходит их переориентация во внешнем магнитном поле H. Затрачиваемая на это работа dW_м =Z_м H·de (где Z_м – модуль вектора намагничивания Z_м ) также может быть представлена в виде произведения действующего на магнитный диполь крутящего момента M_Н на угол его поворота dφ_м . Таким образом, в электрических и магнитных полях помимо центральных сил всегда можно выделить ориентационную составляющую, действующую на тела с несферической симметрией. Это относится в полной мере и к гравитационным полям. Рассмотрим, например, потенциальную энергию U(r) гантели с массой грузов m и расстоянием между ними l, расположенных в поле тяжести Земли с массой М на расстоянии r:

E₁ (r) = –2GMm/r, (3)

где G – гравитационная постоянная.

Однако, если тот же стержень повернуть вокруг неподвижного центра масс в вертикальное положение, координаты центров массы его половинок будут равны соответственно:

r₁ = r + l/2 и r₂ = r – l/2,

а потенциальная энергия примет значение:

E₂ (r) = –GMm[1/(r + l/2) + 1/(r – l/2)], (4)

т.е. изменится на величину:

E₂ (r) – E₁ (r) = –(2GMm/r)[l/(r – l/2) + l/(r + l/2)]. (5)

Отсюда следует, что поворот в поле тяжести тел с несферической симметрией также требует затраты некоторой работы, связанной с переходом потенциальной энергии центральных сил в ориентационную энергию и обратно. Таким образом, ориентационная составляющая потенциальной энергии систем присуща в принципе всем известным силовым полям. Существование наряду с полем центральных сил F_k поля моментов M_k приводит к тому, что потенциальная энергия тела U=U(r, φ) включает в себя в общем случае две составляющие, зависящие соответственно от положения тела U=U(r) и его ориентации U=U(φ). Это означает, что потенциальная энергия силовых полей является в общем случае функцией шести переменных – трех координат центра инерции и трех углов, определяющих ориентацию тела относительно неподвижной системы отсчета [7].

Ориентационная энергия спиновых систем

Вывод о существовании ориентационной составляющей энергии выглядел бы достаточно банальным, если бы он относился только к известным силовым полям. Значительно интереснее показать, что эта составляющая энергии присуща и вращающимся телам независимо от наличия у них упомянутых выше форм энергии. С этой целью рассмотрим систему вращающихся тел с несферической симметрией (уравновешенный волчок или гироскоп – центр тяжести которого совпадает с центром подвеса). Предположим, что момент количества движения любого k-го тела такой системы L_k по каким-либо причинам не совпадает с собственной осью его вращения, так что оно помимо вращения вокруг собственной оси с постоянной угловой скоростью Ω_k испытывает регулярную прецессию с угловой скоростью ω_k относительно направления вектора момента его количества движения L_k (рис.1).

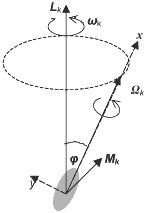
Рис. 1.

Воспользовавшись произвольностью выбора осей координат, совместим вслед за [2] ось x с осью симметрии волчка, а ось y – с плоскостью, образованной векторами L_k и Ω_k , как это показано на рисунке. Тогда угловая скорость вращения волчка вокруг собственной оси Ω_k = |Ω_k | и угловая скорость его прецессии ω_k =|ω_k | определятся соотношением [2]:

Ω_k = L_k cosφ/I_x ; ω_k = L_k /I_y , (6)

где L_k = |L_k |; I_x , I_y – моменты инерции волчка относительно осей x и y; φ – угол, образованный векторами L_k и Ω_k .

Этим угловым скоростям соответствуют кинетические энергии собственного E_k ^c и прецессионного E_k ^п вращения, равные:

E_k ^c = L_k ² cos² φ/2I_x ; E_k ^п = L_k ² /2I_y . (7)

Таким образом, суммарная кинетическая энергия рассматриваемого волчка

E_k = E_k ^c + E_k ^п = ΔE_k = L_k ² (cos² φ + I_x /I_y )/2I_x , (8)

является в общем случае функцией не только количества движения L_k , но и угла φ, определяющего ориентацию оси его собственного вращения в пространстве E_k =E_k (L_k ,φ).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--