Реферат: Обчислення визначеного інтеграла функції F на відрізку A B за формулою Сімпсона
За узагальненою формулою Сімпсона обчислимо наближене значення інтеграла (6.19) з кроком n=0,1 і оцінимо повну абсолютну похибку D1.
Користуючись таблицею 6.1, за формулою (6.33) знайдемо :
Ісм=0,38177448»0,381745
Щоб оцінити залишковий член R(f) формули Сімпсона за формулою (6.35), треба знайти похідну четвертого порядку від функції f(x)=xcosx, маємо
f’’’’(x)=4sinx+xcosx, звідси
![]()
Тому для залишкового члена R(f) за формулою (6.35) (a=0, b=1, h=0,1, M4=5) дістанемо ![]()
Похибка остаточного округлення Do=0,2*10^(-7), а неусувна похибка ![]() Df
Df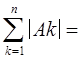 Df
Df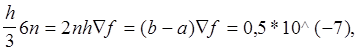 бо
бо 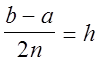 , а значення підінтегральної функції f у вузлах Xk (k=0,1,...10) обчислювали з точністю 0,5*10^(-7), тобто Df=0,5*10^(-7).
, а значення підінтегральної функції f у вузлах Xk (k=0,1,...10) обчислювали з точністю 0,5*10^(-7), тобто Df=0,5*10^(-7).
За формулою (6.3) для повної абсолютної похибки чисельного інтегрування функції f(x)=xcosx знаходимо таку оцінку :
D1=0,278*10^(-5)+0,5*10^(-7)+0,2*10^(-7)=0,285*10^(-5)<0,3*10^(-5).
Отже обчислене за формулою Сімпсона для n=10,h=0,1 наближене значення інтеграла (6.19) має п’ять правильних значущих значущих цифр, тобто
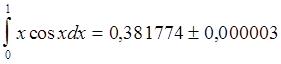
Найбільший внесок у повну абсолютну похибку узагальненої формули Сімпсона вносить залишковий член R(f). Тому для визначення кількості відрізків n-розбиття [a;b], яке гарантує обчислення наближеного значення інтеграла з точністю E>0, досить скористатись формулою (6.36). Звичайно, всі проміжні обчислення при цьому слід проводити з точністю, більшою за E. Наприклад, щоб обчислити наближене значення інтеграла (6.19) з точністю E=0,5*10^(-4), треба відрізок [0;1] поділити не меньш як на три рівні частини, бо за формулою (6.36) ( а=0, в=1, М4=5 ) маємо ![]()
Обчислимо інтеграл (6.19) за формулою (6.33), поклавши n = 2, 4, 8, 16. Знайдемо І2 = 0,38182200; І4=0,38177633; І8=0,381773333. А це означає, що І2 має три, І4 - п‘ять, І8 - шість правильних значущих десяткових цифр. В І16 - всі 8 цифр правильні.
2. Метод Сімпсона.
Власне значення інтеграла
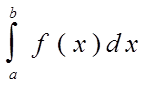
можна знайти методом Сімпсона (парабол). Для цього відрізок [a,b] розбивається на n=2m частин Co=A,C1=A+h,...,Cn=В з кроком h=(b-a)/n (1)
У точках Хі обчислюють значення функції У1=f(Xi) і знаходять наближене значення інтеграла за формулою Сімпсона S = Sn + Rn
де ![]()
![]()
![]()
![]()
Далі кількість точок розбиття подвоюється і здійснюється оцінка точності обчислень
![]()
Якщо ![]() , то кількість точок розбиття знову подвоюється. При цьому значення суми 2*(у1+у2+...+у2m-1) у попередніх точках розбиття зберігається, тому для обчислення інтеграла при подвоєнні кількості точок розбиття треба обчислювати значення у(х) лише в нових точках.
, то кількість точок розбиття знову подвоюється. При цьому значення суми 2*(у1+у2+...+у2m-1) у попередніх точках розбиття зберігається, тому для обчислення інтеграла при подвоєнні кількості точок розбиття треба обчислювати значення у(х) лише в нових точках.
4.ДОДАТКИ :
4.1.Додаток 1: Структура програми.
У даній програмі використовуються змінні :
а, в - межі інтегрування;
е - точність;
х - аргумент функції f(x);
h - крок;