Реферат: Обчислення визначеного інтеграла функції F на відрізку A B за формулою Сімпсона

x1=xi+h.

Контрольний приклад.

Інтеграл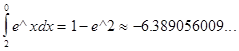

Функція ff(x) має вигляд :

Function ff( x:Real ):Real;

Begin ff:=exp(x) END;

Структура програми

1-2 - заголовок функції та опис локальних змінних;

4-11 - обчислення за формулами (2) і (3)

Програма. Інтеграл за Сімпсоном.

FUNCTION FF(X:REAL):REAL;

BEGIN FF:=EXP(X) END;

FUNCTION Simpson(a,b,e:real):real;

var h,S,S1,S2,S3,X,X1:REAL;

BEGIN

S2:=1E+30;H:=B-A;S:=FF(A)+FF(B);

REPEAT

S3:=S2;H:=H/2;S1:=0;X1:=A+H;

WHILE(X1>B)=(H<0) DO

BEGIN S1:=S1+2*FF(X1);X1:=X1+2*H;

END;

S:=S+S1;S2:=(S+S1)*H/3;X:=ABS(S3-S2)/15

UNTIL X<E;

SIMPSON:=S2; END;

4.2.Додаток 2. : Узагальнення проекту.

На даний момент існує досить багато різних методів в математичній галузі чисельного інтегрування функцій. До найвідоміших методів відносяться :

а) Квадратурні формули Ньютона-Котеса;

б) Формула прямокутників;

в) Формула трапецій;