Реферат: Обработка результатов эксперимента
1
0,02
[22;23)
56
[-0,57;0,04)
0,231
57,75
3,06
0,05
[23;24)
60
[0,04;0,64)
0,223
55,75
18,06
0,32
[24;25)
38
[0,64;1,25)
0,154
38,50
0,25
0,01
[25;26)
16
[1,25;1,85)
0,074
18,50
6,25
0,34
[26;27)
7
[1,85;2,46)
0,025
6,25
0,56
0,09
[27;28]
2
[2,46;+∞)
0,007
1,75
0,06
0,03
250
1.000
250,0
Замечание. Наименьшее значение стандартизованной переменной 
заменено 
, наибольшее значение 
заменено 
. Эта замена произведена для того, чтобы сумма теоретических (модельных) частот npi была равна объему выборки.
В результате вычислений получили 
. Найдем по таблице квантилей 
распределения по уровню значимости α = 0,05 и числу степеней 
критическое значение 
. Так как 
, то нет оснований для отклонения гипотезы о нормальном распределении прочности бетона на сжатие.
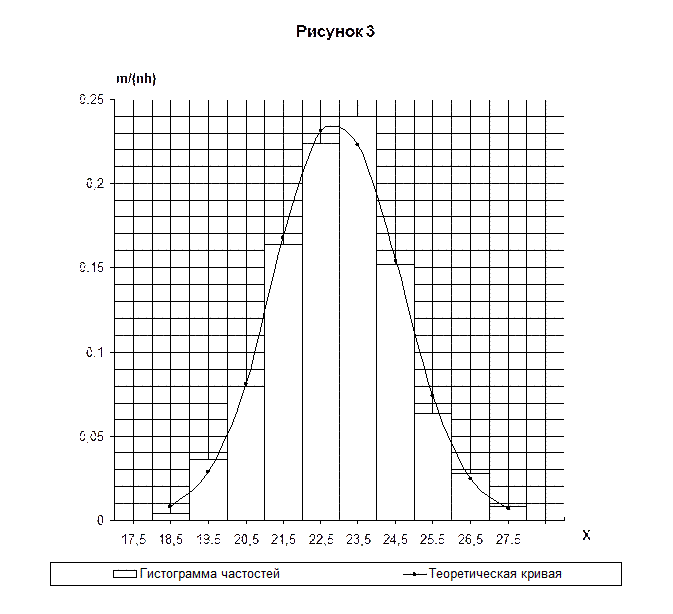
Построим нормальную кривую. Для этого из середин частичных интервалов восстании перпендикуляры высотой pi / h (p i — вероятность попадания СВ Х в частичный интервал; h — длина интервала). На рисунке 3 концы этих перпендикуляров отмечены кружками. Полученные точки соединены плавной кривой. Сравнение гистограммы и нормальной кривой наглядно показывает, что нормальная кривая хорошо сглаживает гистограмму относительных частот.
Найдем интервальные оценки параметров нормального распределения. Для вычисления доверительного интервала накрывающего математическое ожидание прочности бетона на сжатие (СВ Х), найдем по таблицам квантилей распределения Стьюдента по заданной доверительной вероятности 
и числу степеней свободы‚ 
квантиль
.
Вычислим предельную погрешность интервального оценивания
Искомый доверительный интервал для математического ожидания
Смысл полученного результата: если будет произведено достаточно большое число выборок по 250 исследований прочности образцов бетона на сжатие, то в 95% из них доверительный интервал накроет математическое ожидание прочности бетона и только в 5% случаев математическое ожидание может выйти за границы доверительного интервала.
Для нахождения доверительного интервала, накрывающего неизвестное среднее квадратическое отклонение σ с заданной вероятностью 
, найдем по доверительной вероятности 
и числу степеней свободы ‚ два числа; 
. Искомый доверительный интервал
Полученный результат означает, что если будет произведено достаточно большое число выборок по 250 исследований прочности образцов бетона на сжатие, то в 95% из них доверительный интервал накроет среднее квадратическое отклонение σ и только в 5% среднее квадратическое отклонение σ можёт выйти за границы доверительного интервала.