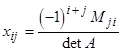,

где М_ji - дополнит ельный минор элемента а_ji матрицы А.

Пример. Дана матрица А = , найти А^-1 .

det A = 4 - 6 = -2.

M₁₁ =4; M₁₂ = 3; M₂₁ = 2; M₂₂ =1

x₁₁ = -2; x₁₂ = 1; x₂₁ = 3/2; x₂₂ = -1/2

Таким образом, А^-1 =.

Cвойства обратных матриц

Укажем следующие свойства обратных матриц:

(A^-1 )^-1 = A;

(AB)^-1 = B^-1 A^-1

(A^T )^-1 = (A^-1 )^T .

Пример. Дана матрица А = , найти А³ .

А² = АА = = ; A³ = = .

Отметим, что матрицы и являются перестановочными.

Пример. Вычислить определитель .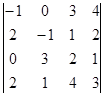

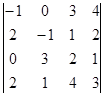= -1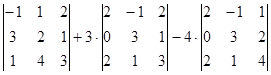

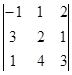= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.

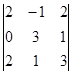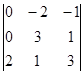= = 2(0 – 2) – 1(0 – 6) = 2.

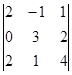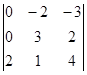= = 2(-4) – 3(-6) = -8 + 18 = 10.

Значение определителя: -10 + 6 – 40 = -44.

Базисный минор матрицы

Ранг матрицы

Как было сказано выш е, минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении каких - либо выбранных s строк и s столбцов.

Определение. В матрице порядка m´n минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.

Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.

В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.

Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А.

Очень важным свойством элементарны х преобразований матриц является то, что они не изменяют ранг матрицы.

Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.

Надо отметить, что равные матрицы и эвивалентные матрицы - понятия совершенно различные.