Любое такое решение описывает "сверхпроводящее" или "стационарное" S -состояние джозефсоновского перехода: при протекании не слишком большого тока падение напряжения на переходе отсутствует:

(20)

Факт существования S -состояния получил специальное название "стационарный эффект Джозефсона". Если же постоянный ток I превышает критическое значениеI_C , то он, согласно формуле (5), уже не может полностью переноситься сверхтоком I _S , и, следовательно, часть его должна переноситься нормальным током I_N . Однако I_N может быть отличен от нуля лишь при . Таким образом, по крайней мере при │ I │> I_C переход может находиться только в резистивном (R) состоянии, в котором среднее напряжение отлично от нуля, и, следовательно, происходит процесс генерации с частотой

(21)

Это явление называется "нестационарным эффектом Джозефсона" или "джозефсоновской генерацией".

У вольтамперной характеристики при │ I │< I_C будет "сверхпро-водящая" или "S -ветвь", а при │ I │> I_C - резистивная или " R-ветвь":

при (22)

При │ I │> I_C существуют лишь резистивные состояния.

Ограничиваясь в данном разделе случаем контактов с малой емкостью, рассмотрим следующее уравнение движения фазы:

(23)

Решение ищем численным методом Хюна:

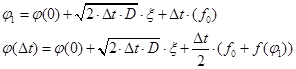(24)

где .

В отсутствии флуктуаций, R-ветвь ВАХ будет иметь гиперболическую форму (рис.3). Если же учесть флуктуации тока, то на вольтамперной характеристике при токах │ I │< I _С появляется напряжение, отличное от нуля.

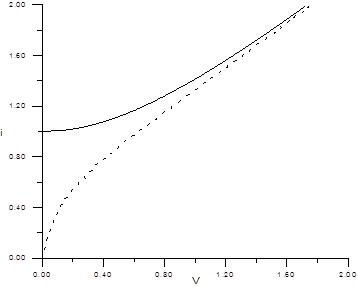
Рис.3. Вольтамперная характеристика джозефсоновского контакта. Сплошная линия - без учета флуктуаций D= 0, пунктирная D=0.5

При слабом высокочастотном воздействии (амплитуда А тока, воздействующего на переход, достаточно мала) внешний сигнал с частотой может производить захватывание (синхронизацию) джозефсоновских колебаний перехода. Это явление сопровождается появлением на ВАХ перехода горизонтального участка - "джозефсоновской ступеньки тока" - при напряжениях

(25)

Вид ВАХ перехода в таком режиме будет рассмотрен в главе об СВЧ СКВИДе.

1.3 Устройство фазового кубита

Любая квантовая двухуровневая система имеет основное |0ñ и не основное |1ñ базисные состояния. При этом волновая функция состояний двухуровневой системы - квантового бита, может представлять собой суперпозицию базисных состояний следующего вида |yñ = a|0ñ + b|1ñ, где a,b - комплексные амплитуды состояний, | a |² + | b |² = 1 . Помимо вероятностей P (0) = | a |² и P (1) = | b |² , заполнения базисных состояний |0ñ и |1ñ, состояние кубита характеризуется когерентными или интерференционными слагаемыми в вероятности состояния |yñ, определяемых произведениями комплексных амплитуд ab^* и a^* b.

Принципиальная схема работы любого квантового компьютера может быть представлена следующим образом (рис.4). Основной его частью является квантовый регистр - совокупность некоторого числа L кубитов. До ввода информации в компьютер все кубиты регистра должны быть приведены в основные базисные (булевые) состояния. Эта операция называется подготовкой начального состояния или инициализацией (initializing). Далее каждый кубит подвергается селективному воздействию, например, с помощью импульсов внешнего электромагнитного поля, управляемых классическим компьютером, которое переведет основные базисные состояния определенных кубитов в не основное состояние |0ñ  |1ñ. При этом состояние всего регистра перейдет в суперпозицию базисных состояний вида |n ñ = |n ₁ ,n ₂ ,n ₃ ,. n _L ñ, где n _i = 0,1.

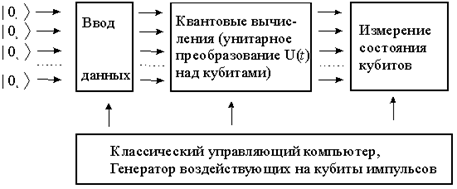
Рис.4. Схематическая структура квантового компьютера

При вводе информации в квантовый компьютер состояние входного регистра, с помощью соответствующих импульсных воздействий преобразуется в соответствующую когерентную суперпозицию базисных ортогональных состояний. В таком виде информация далее подвергается воздействию квантового процессора, выполняющего последовательность квантовых логических операций, определяемую унитарным преобразованием, действующим на состояние всего регистра. К моменту времени t в результате преобразований исходное квантовое состояние становится новой суперпозицией, которая и определяет результат преобразования информации на выходе компьютера.

Считается, что для реализации полномасштабного квантового компьютера, превосходящего по производительности любой классический компьютер, на каких бы физических принципах он не работал, следует обеспечить выполнение несколькихосновных требований. Одно из основных требований и задач квантовых вычислений - проблема измерения конечного квантового состояния.

Рассмотрим кубит, основанный на использовании джозефсоновских переходов. Джозефсоновские переходы представляют собой некоторую слабую электрическую связь между двумя сверхпроводниками. Все сверхпроводящие электроны образуют связанные парные состояния, получившие название куперовских пар электронов. Куперовская пара объединяет два электрона с противоположными спинами и импульсами и, следовательно, имеет нулевой суммарный спин. Вся совокупность (конденсат) куперовских пар является когерентной, то есть описывается в квантовой механике единой волновой функцией.

На рис.5 представлена схема фазового кубита [3] (управление кубитом осуществляется на основе фазы волновой функции, а не числа куперовских пар).

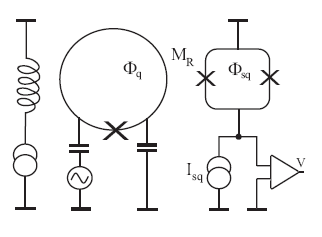
Рис.5. Схема фазового кубита