Реферат: Основи теорії експлуатації і надійності електронної побутової апаратури

- середній термін зберігання –

- гамма-відсотковий термін зберігання –

5. Показники готовності:

- коефіцієнт готовності –

- коефіцієнт оперативної готовності –

- коефіцієнт технічного використання –

6. Експлуатаційно-технічні показники:

- середня трудомісткість поточного ремонту –

- середня трудомісткість технічного обслуговування –

- коефіцієнт вартості експлуатації –

3. Основні поняття теорії ймовірності

Виникнення відмов в ЕА залежить від різних факторів, які визначаються як внутрішніми властивостями апаратури, так і діями зовнішніх умов. Це призводить до того, що процес виникнення відмов, а також інші характеристики ЕА у процесі експлуатації носять випадковий характер. Тому для кількісної оцінки різних характеристик ЕА широко використовуються імовірнісні методи.

У теорії ймовірності випадковою називається величина, яка в результаті експерименту може прийняти те або інше значення, передбачити яке заздалегідь вірогідно неможливо. Всі випадкові величини поділяються на безперервні та дискретні. Прикладами безперервних випадкових величин є час безвідмовної роботи пристрою, значення того або іншого технічного параметра тощо.

Дискретними випадковими величинами є кількість відмов, які виникають за деякий період роботи пристрою, кількість несправних елементів, пристроїв тощо.

Подією в теорії ймовірності визначається будь-який факт, який у результаті експерименту може статися або не статися. Для кількісного порівняння подій між собою за ступенем їх можливості використовують визначене число, яке тим більше, чим більш можлива подія. Таке число називають ймовірністю події.

Якщо ймовірність однієї події не змінюється від того, відбулась чи ні друга подія, то така подія називається незалежною. Якщо ж можливість появи однієї події залежить від того, відбулась чи ні друга подія, то такі події називають залежними. Події називаються несумісними, якщо ніякі дві з них не можуть з’явитися разом.

Подію, ймовірність якої дорівнює одиниці, називають вірогідною подією. Подію, ймовірність якої близька до одиниці, називають практично ймовірною.

На основі введеного поняття розглянемо основні теореми теорії ймовірності, які широко застосовуються під час вирішення багатьох задач надійності.

3.1 Теореми додавання та множення ймовірностей

Ймовірність суми n несумісних подій дорівнює сумі ймовірностей цих подій:

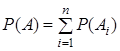. (1)

Ймовірність добутку незалежних подій дорівнює добутку ймовірностей цих подій:

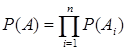. (2)

На практиці рідко зустрічаються задачі, в яких потрібно застосовувати тільки теорему додавання або тільки теорему множення ймовірностей. Як правило, ці теореми застосовують спільно.

3.2 Теорема повної ймовірності

На основі теореми додавання та множення формулюється теорема повної ймовірності.

Нехай потрібно визначити ймовірність деякої події А, яка може відбутися разом з однією з подій , що утворюють групу несумісних подій, які називаються гіпотезами:

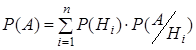,(3)

тобто ймовірність події А знаходиться як сума добутків ймовірностей кожної гіпотези на ймовірність події при цій гіпотезі.