Реферат: Основи теорії експлуатації і надійності електронної побутової апаратури

Законом розподілу випадкової величини називають співвідношення, яке встановлює зв’язок між можливим значенням випадкової величини та відповідними їм ймовірностями. Вважають, що випадкова величина в цьому випадку підпорядкована даному закону розподілу.

Інтегральним законом розподілу або функцією розподілу називається функція виду:

(4)

де x – деяка поточна змінна.

Функція розподілу – універсальна характеристика випадкової величини. Вона існує як для перервних, так і безперервних величин і характеризує ймовірність події Х<x. Функція розподілу має такі властивості:

- функція розподілу F(x) є функція, яка не зменшується від свого аргументу, тобто при х₂ >x₁ , F(x₂ )≥F(x₁ );

- на мінус нескінченності функція розподілу дорівнює нулю F(-∞)=0;

- на плюс нескінченності функція розподілу дорівнює одиниці F(∞)=

Нехай маємо випадкову величину Х з функцією розподілу F(x), яку припускаємо безперервною та диференційованою. Обрахуємо ймовірність натрапляння цієї випадкової величини у відрізок від х до х+Δх. Умовимося лівий кінець відрізку х включати в інтервал х, х+Δх, а правий – не включати. Тоді потрапляння випадкової величини Х у відрізок х, х+Δх рівносильне виконанню нерівності:

Виразимо ймовірність цієї події через F(x). Для цього розглянемо три події:

- подія А полягає в тому, що Х<x+Δx;

- подія В полягає в тому, що Х<x;

- подія С полягає в тому, що х≤ Х<x+Δx.

Враховуючи, що А=В+С, згідно з теоремою додавання ймовірностей отримаємо:

або

звідки

тобто отримати приріст функції розподілу на цьому відрізку.

Отже, ймовірність потрапляння випадкової величини у заданий інтервал дорівнює приросту функції розподілу на цьому інтервалі.

Розглянемо відношення (частку) цієї ймовірності до довжини інтервалу та наближатимемо Δx до нуля.

На границі ми отримаємо похідну від функції розподілу:

(5)

Функція f(x) – похідна функції розподілу, характеризує щільність, з якою розподіляється значення випадкової величини у даній точці. Ця функція називається щільністю розподілу або диференціальним законом розподілу величини Х. Щільність розподілу є однією з форм закону розподілу. На противагу функції розподілу щільність існує тільки для безперервних випадкових величин.

Кожен закон розподілу являє собою деяку функцію, яка повністю описує випадкову величину з імовірнісної точки зору. Проте часто на практиці немає необхідності характеризувати випадкову величину повністю, буває достатньо лише знати окремі числові параметри. Такі параметри, які характеризують у стислій формі істотні особливості розподілу, називаються числовими характеристиками випадкової величини. Основними числовими характеристиками випадкових величин, які вивчають у надійності, є математичне сподівання або середнє значення та дисперсія.

Для перервної величини Х математичним сподіванням називається сума добутків усіх можливих значень випадкової величини на ймовірність цих значень:

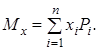(6)

Для безперервної величини Х математичне сподівання виражається вже не сумою, а інтегралом:

(7)