Реферат: Основная теорема алгебры
|a0 xn |>k|a1 xn-1 +a2 xn-2 +….+an | (2)
Доказательсво.
Пусть А=max(![]() ), тогда
), тогда
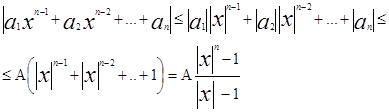
пологая |x| >1, получим
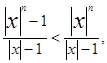
откуда
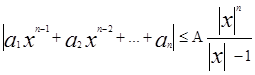
следовательно неравенство (2) будет выполняться если |x|>1 и
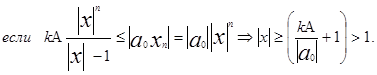
Лемма №2 доказана.
Лемма №3 .
![]()
Доказательство.
![]() (3)
(3)
применим лемму 2: при k=2 существует такое N1 , что при |x|> N1
|a0 xn |>2|a1 xn-1 +a2 xn-2 +….+an |
откуда
|a1 xn-1 +a2 xn-2 +….+an |<|a0 xn |/2
тогда из (3)
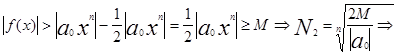
при |x|>N=max(N1 ,N2 ) |f(x)|>M что и тебовалось доказать.
Лемма №3(Лемма Даламбера).
Если при x=x0 многочлен f(x) степени n ,![]() не обращаеться в нуль, то существует такое приращение h, в общем случае комплексное, что
не обращаеться в нуль, то существует такое приращение h, в общем случае комплексное, что
|f(x0 +h)|<|f(x)|
Доказательство.
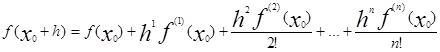
По условию f(x0 ) не равно нулю, случайно может быть так, что x0 является корнем f’(x),..,f(k-1) (x). Пусть k-я производная будет первой, не имеющей x0 своим корнем. Такое k существует т.к.
f(n) ( x0 )=n!a0
Таким образом
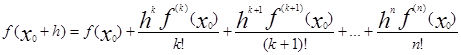 |
?.? f(x0 ) ?? ????? ???? ?? ??????? ??? ????? ????????? ?? f(x0 )