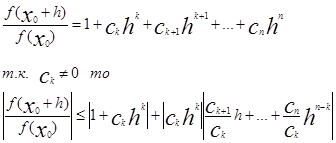
Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и его аргумент.

По лемме№1:

С другой стороны при

(4)

Пусть |h|<min(б₁ , б₂ ), тогда

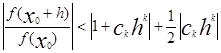
Теперь выберем аргумент h так, чтобы c_k h^k было действительным отрицательным числом.

При таком выборе c_k h^k =-| c_k h^k | следовательно учитывая (4) получим

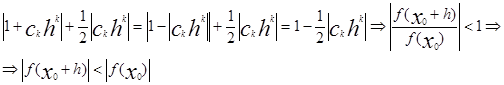
Что доказывает лемму Даламбера.

Лемма №5.

Если действительная функция комплексного переменного f(x) непрерывна в замкнутом круге Е, то она ограничена.

Доказательство.

Предположим, что это не верно тогда

получена бесконечная ограниченная последовательность x_n ,

из нее можно выбрать сходящуюся подпоследовательность , пусть ее предел равенx₀ . Так как круг Е замкнут, то x₀ пренадлежит Е. Тогда так как f(x) непрерывна

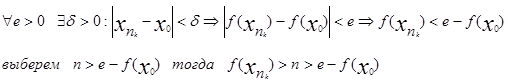
получено противоречие, следовательно неверно, предположение о неограничености f(x) .

Лемма №6.

Действительная функция комплексного переменногоf(x) непрерывная в замкнутом круге Е достигает своего минимума и

максимума.

Доказательство.

Докажем это утверждение для максимума.

Так как f(x) непрерывна в Е, то она ограничена и следовательно существует M =sup{ f(x)} . Рассмотрим функцию .

Если f(x) не достигает своего максимума, то M> f(x) следовательно M- f(x)>0 , следовательно g(x) непрерывна в Е.

Полученое противоречит тому, что M =sup{ f(x)} . Следовательно функция достигает свего максимума. Аналогично доказывается достижение минимума.

Доказательство основной теоремы.