Реферат: Основная теорема алгебры
Всякий многочлен с любыми комплексными коэффициентами , степень которого не меньше единицы имеет хотя бы один корень, в общем случае комплексный.
План доказательства .
Лемма №1 . Многочлен f(x) является непрерывной функцией комплексного переменного x .
Лемма №2 . Если данн многочлен n -ой степени, n>0,
f(x)=a0 xn +a1 xn-1 +…+an
с произвольными комплексными коэффициентами и если k - любое положительное действительное число, то для достаточно больших по модулю значений
|an xn |>k|axn-1 +an xn-2 +….+a0 |
Лемма №3 . ![]()
Лемма №4 .(Лемма Даламбера).
![]()
Лемма №5.
Если действительная функция комплексного переменного f(x) непрерывна в замкнутом круге Е, то она ограничена.
Лемма №6.
Действительная функция комплексного переменного f(x) непрерывная в замкнутом круге Е достигает своего минимума и максимума.
Доказательство основной теоремы .
Лемма №1.
Надо доказать, что ![]() |f(x0 +x)-f(x0 ) |<e .
|f(x0 +x)-f(x0 ) |<e .
Докажем Лемму №1 сначала для многочлена без свободного члена и при x0 =0
Если A=max(|a0 |,|a1 |,…,|a n-1 |) и ![]() (1)
(1)
то |f(x)|=|a0 xn +…+an-1 x| ![]()
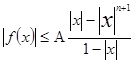 |
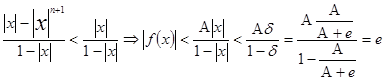 |
?.? |x |<б , ? ?? (1) б <1, ??
т.к. a0 =0 то f(0)=0 ![]()
Что и требовалось доказать.
Теперь докажем непрерывность любого многочлена.
f(x0 +x)=a0 (x0 +x)n +…+an
pаскрывая все скобки по формуле бинома и собирая вместе члены с
одинаковыми степенями x получим
![]()
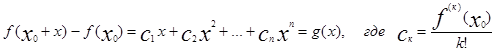
Многочлен g(x)-это многочлен от x при x0 =0 и а0 =0 ![]() |f(x0 +x)-f(x)|=|g(x)|<e
|f(x0 +x)-f(x)|=|g(x)|<e
Лемма доказана.
Лемма №2
Если дан многочлен n -ой степени, n>0,
f(x)=a0 xn +a1 xn-1 +…+an
--> ЧИТАТЬ ПОЛНОСТЬЮ <--