Реферат: Основные элементарные функции, их свойства и графики

График функции у = соs (х) изображен на рисунке 12.

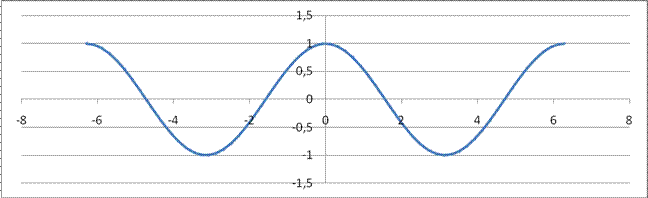
Рис. 12 График функции ; на интервале xÎ [-2;2]

Функция y = tg х.

1. Область определения: D(x) Ï π/2 + πk, kÎZ.

2. Область значений E(y) Î (- ∞; + ∞)

3. π- основной период функции.

4. Функция нечетная.

5. Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn).

График функции у = tg х изображен на рисунке 13.

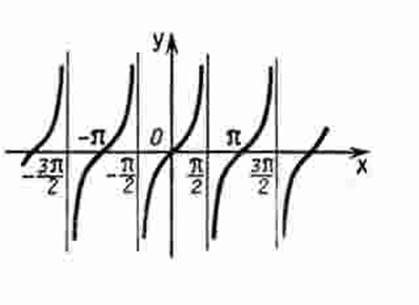
Рис. 13 График функции ; на интервале xÎ (- ;)

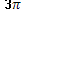Функция y = ctg х.

1. Область определения функции: D(x) Ï xπ/2 +πk, kÎZ.

2. Область значений функции E(y) Î (- ∞; + ∞).

3. Функция периодическая с основным периодом π.

4. Функция нечетная.

5. Функция у = ctg х убывает на промежутках (πn;π+πn).

График функции у = ctg х изображен на рисунке 14.

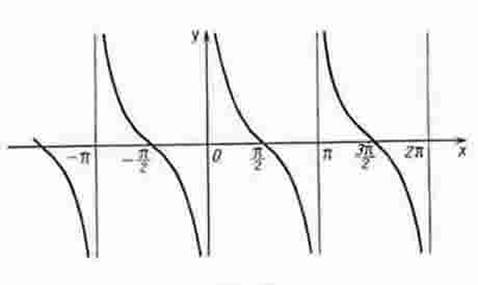
Рис. 14 График функции ; на интервале xÎ (-𝜋;)

Обратные тригонометрические функции:

Функции y = arcsin (х), у = arccos (х), у = arctg (х), у = arcctg (х) называют обратными тригонометрическими функциями.

Функция y = arcsin ( x ):

Свойства функции y = arcsin (x):

1. Область определения D(x)Î[−1;1]

2. Область значения E(y)Î [−π/2;π/2]

3. y=arcsin(x)- непрерывная строговозрастающая функция на D

5. График y = arcsin(x) симметричен графику y = sin(x) относительно линии y=x

6. y=arcsin(x) нечетная функция т.е. ∀x∈[−1;1] arcsin(−x)=−arcsin(х)