Реферат: Основные характеристики пространственной структуры излучения

До сих пор при изложении вопросов обнаружения сигналов на фоне помех учитывалась только их временная структура. В то же время как сигналы, так и помехи являются электромагнитными полями, которые характеризуются амплитудными и фазовыми распределениями на раскрыве передающей или приемной антенны, где x,y - координаты раскрыва.

Под пространством сигнала будем понимать для определенности плоскость (x,y). На плоскости (x,y) в пределах площадисуществует поле f(x,y,t), а внеполе равно нулю (рис. 2.9.1)

где A(x,y,t) и - амплитуда и фаза поля.

Пусть пространственный сигнал f(x,y) представляет распределение на плоскости Z = 0, т.е. на плоскости (x,y), амплитуд и фаз поля монохроматического колебания

,

где - амплитуда, круговая частота и начальная фаза монохроматического колебания.

При этом поле в полусфере бесконечного радиуса при Z > 0, опирающейся на плоскости Z = 0, является суммой плоских волн с различными амплитудами, фазами и направлениями распространения:

Рис. 1. Пространство сигнала.

Рис. 2. Проекции волнового вектора на координатные оси.

где - радиус-вектор, проведенный из начала координат в точку наблюдения;

- волновой вектор, модуль которого

;

- проекция волнового вектора;

- комплексная функция, которая описывает амплитуду и фазу отдельной плоской волны с направлением распространения, определяемым совокупностью двух действительных переменных и .

Заметим, что факт распространения плоской волны в любом направлении отражается условием сохранения фазы волнового фронта, распространяющегося со скоростью света С :

, если

.

Факт суммирования плоских волн, распространяющихся во всех направлениях передней полусферы, отражается их двойным интегрированием по всем направлениям.

Направление распространения волна определяется проекциями волнового вектора на координатные оси (рис.2). В общем случае направление распространения волны определяется двумя углами и . Если эти углы выбраны по отношению к прямоугольной системе координат x, y, z так, как показано на рис. 2, то

,

.

Так как три проекции волнового вектора связаны соотношением , то независимых проекций всего две - и , а третья проекция

.

Используя введенные обозначения, перепишем выражение для искомого поля так

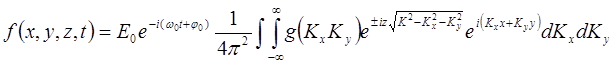Определим комплексную функцию . Очевидно, что приведенное решение волнового уравнения должно удовлетворять следующему условию – на плоскости Z=0 это решение должно иметь вид заданного пространственного сигнала

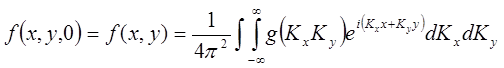
Полученное выражение представляет собой обратное двумерное преобразование Фурье. Прямое двумерное преобразование Фурье позволяет найти функцию :

--> ЧИТАТЬ ПОЛНОСТЬЮ <--