Реферат: Основные характеристики пространственной структуры излучения

Учитывая это, фазочастотная характеристика свободного пространства может приближенно рассматриваться в различных условиях дифракции:

1) в условиях приближения геометрической оптики изменением ФЧХ свободного пространства в диапазоне углов дифракции можно пренебречь

Рис. 3. Фазочастотная характеристика свободного пространства.

Рис. 4. Диаграмма направленности антенны при равномерном АФР.

,

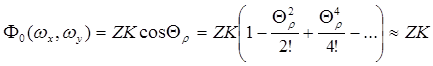если второе (отброшенное) слагаемое разложения в ряд Маклорена много меньше радиан

,

что выполняется в области глубокой ближней зоны

.

2) в условиях дифракции Френеля фазочастотную характеристику свободного пространства в диапазоне углов дифракции можно аппроксимировать параболой

,

если третье (отброшенное) слагаемое разложения в ряд Маклорена много меньше радиан

,

что выполняется на расстояниях

т.е. практически в области ближней зоны

.

3) в условиях дифракции Фраунгофера, когда изменение фазочастотной характеристики свободного пространства в диапазоне углов рефракции больше радиан

т.е. практически в области дальней зоны

.

При этом решение дифракционной задачи упрощается в большей мере, чем даже в частных случаях дифракции Френеля или приближения геометрической оптики. Действительно, поле в дальней зоне, используя полярную систему координат

,

,

,

можно представить в следующем виде:

.

Учитывая ограниченную область изменения пространственной частоты , относительно малые размеры пространства сигнала , относительно небольшой диапазон изменения углов дифракции , можно вычислить интеграл путем ряда уточнений, преобразований переменной интегрирования упрощений: