Реферат: Основные положения дискретной математики

Транзитивность: из aRb и bRс следует aRс данное условие мы проверит не можем, т. к. оно применимо только для трех или более элементов.

1.7 Декартово произведение множеств

Декартовым произведением – XY множеств X и Y называется множество М вида

В круглых скобках обозначена последовательность, т. е. множество, в котором зафиксирован порядок элементов.

Подмножество FXY называется функцией, если для каждого элемента xX, найдется не более одного элемента yY вида (x,y)F; при этом, если для каждого элемента х имеется один элемент y вида (x,y)F, то функция называется всюду (полностью) определенной, в противном случае – частично определенной (не доопределенной).

Множество Х образует область определения функции F.

Множество Y образует область значений функции F.

Часто вместо (x,y)F пишут у=F(х), при этом элемент х называется аргументом или переменной, а у – значением функции F.

Сопоставим с декартовым произведением двух множеств х=. и у=. прямоугольную решетку, узлы которой взаимно однозначно соответствуют элементам декартова произведения (рис.5).

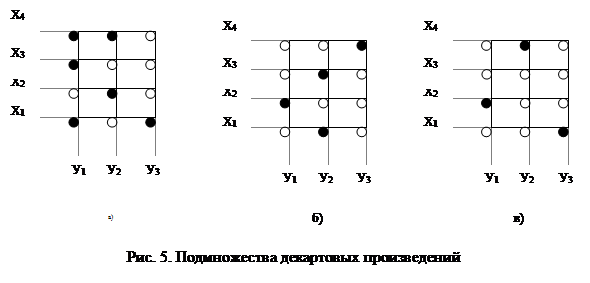
Подмножества декартова произведения обозначены штриховкой соответствующих элементов.

На рис.5 а) показано подмножество декартова произведения не являющееся функцией.

На рис.5 б) показано подмножество декартова произведения, являющееся полностью определенной функцией.

На рис. 5 в) показано подмножество декартова произведения, являющееся частично определенной функцией.

Количество аргументов определяет местность функции. До настоящего момента были рассмотрены одноместные функции.

Аналогично понятию декартова произведения двух множеств можно определить понятие декартова произведения n-множеств.

Декартовым произведением множеств М₁ , М₂ ,…., М_n называется множество Элементами декартова произведения являются всевозможные последовательности, каждая из которых состоит из n элементов, причем первый элемент принадлежит множеству М₁ , второй – множеству М₂ , n-ый – множеству М_{n .}

Если множество М_х в определении функции у=F(x) является декартовым произведением множеств М _х1 , М _х2 ,…., М _{х n} , то получаем определение n-местной функции у=F(х₁ , х₂ ,….,х_n ).

1.8 Функция как отношение

Функцией называется функциональное соответствие.

Если функция f устанавливает соответствие между множествами А и В, то говорят, что функция f имеет тип АВ, обозначается f: АВ. каждому элементу а из своей области определения функция f ставит в соответствие единственный элемент b из области значений. Обозначается f(a)=b.

Элемент а называется аргументом функции, элемент b называется значением функции на а.

Полностью определенная функция f: AB называется отображением А и В.

Областью определения называется выражение D=

Функция называется инъективной, если из отношений (x₁ ,y)f, (x₂ ,y)fx₁ =x₂

Функция называется сюръективной, если для каждого уY существует хХ.

Инъективная и сюръективная функции образуют биекцию – это взаимнооднозначное отношение множеств.

1.9 Отношение порядка

Отношение называется отношением нестрогого порядка, если оно рефлективное, антисимметрично, транзитивно.

Отношение называется отношением строгого порядка, если оно антирефлективное, антисимметрично, транзитивно. Оба типа отношений называются отношениями порядка.

Элементы a,b сравнимы по отношению порядка, если выполняется aRb или bRa. Множество М, на котором задано отношение порядка называется полностью упорядоченным, если любые два элемента множества М сравнимы, в противном случае – частично упорядоченным.

Пример: отношения для чисел являются отношениями нестрого порядка, отношения <,> - отношения строгого порядка. Оба отношения полностью упорядочивают множество. Отношение строгого включения задает строгий частичный порядок: .

Отношение эквивалентности

Отношение называется отношением эквивалентности (эквивалентностью), если оно одновременно рефлективно, симметрично и транзитивно.