Реферат: Основные положения дискретной математики

1. отношение равенства на любом множестве является отношением эквивалентности;

2. утверждение вида (a+b)(b-a)=a² -b² – формулы соединенные знаком равенства задают бинарное отношение. Такое отношение называют отношением равносильности. Оно отличается от равенства, т. к. может выполняться для различных формул.

3. Отношение подобия геометрических фигур, «быть соседями по квартире», «быть ровесниками» так же являются отношениями эквивалентности.

Каждое отношение эквивалентности является в определенном смысле равенством, например, отношение «быть ровесником» означает равенство возрастов.

Задание №3

Какие из перечисленных отношений являются отношениями эквивалентности, а какие – отношениями порядка: <, (на множестве действительных чисел), предшествовать (на множестве слов в словаре), быть однофамильцем (на множестве учащихся в данном вузе).

Решение: необходимо проверить каждое из свойств отношений (аналогично заданию №2) и определить эквивалентность или порядок отношений.

2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Модель является отображением чего-либо. В науке о природе моделирование используется как метод познания.

2.1 Преобразование к модели

1. Эксперимент на модели должен быть проще эксперимента на оригинале.

2. Информация об объекте, полученная в результате эксперимента на модели должна быть переносима на объект.

Существуют различные модели, которые используют в физике и математике.

В физике под моделью понимается реальный объект, в математике модель не обязательно является реальным объектом. однако суть этих моделей одинакова:

-модель должна отражать характеристики и свойства объекта,

-модель должна прогнозировать поведение объекта,

-модель должна быть более простой, чем оригинал, но с другой стороны она должна как можно полнее отражать свойства объекта.

2.2 Способы моделирования

1. Макетное. Широко применяется в строительстве.

2. Физическое. Основой для такого моделирования является теория подобия.

3. Электрическое моделирование.

4. Математическое моделирование.

Мы остановимся на математическом моделировании. Модель представляет собой совокупность зависимостей, позволяющих прогнозировать заданные свойсвта объекта. В математике термин «модель» применяется наряду с обычным толкованием. Может означать, например, теорию подобную другой теории. Математика использует символические модели. Такая модель охватывает определенное множество абстрактных объектов: это числа, векторы и т. д. И отношения между ними.

Математическое отношение – это гипотетическое правило, связывающее между собой два или несколько символических объектов. Многие отношения могут быть выражены с помощью математических операций.

Математическая операция по определенному правилу любым двум элементам множества ставит в соответствие третий элемент, принадлежащий этому же множеству.

Характерным для математической модели может быть отсутствие объектов в физическом мире. Такие абстрактные модели являются отражением физических процессов, например, счет, упорядочение и т. д. Однако математическая модель будет воспроизводить физические стороны объекта, если будут установлены правила соответствия специфических свойств объекта математическим объектам и отношениям.

2.3 Алгебраические модели

Предположим, что объектом изучения являются элементы некоторого множества, о природе и свойствах которого мы ни чего не знаем. Подчиним элементы этого множества операциям, предварительно будем считать, что мы ни чего не знаем об этих операциях, но

3. ТЕОРИЯ КОДИРОВАНИЯ

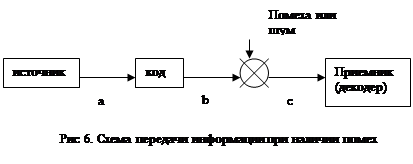
В теории передачи информации существует проблема кодирования – декодирования, обеспечивающая надежную передачу информации при наличии помех.