Реферат: Основные положения синтеза электрических цепей

Математическое расстояние ρ{ξ(x),f(x)} как характеристика близости функций конструируется таким образом, чтобы это было одно единственное положительное число. В теории синтеза ЭЦ обычно используется Чебышевская оценка точности совпадения функций ξ (х) и f (х). (ЧОТС)

При этом математическое расстояние между ξ (х) и f (х) определяется следующим выражением

Геометрический смысл чебышевской оценки точности иллюстрируется графиками (рисунок 1).

В общем случае, при синтезе (проектировании) электрических цепей можно выделить два существенных этапа , которые будут рассмотрены в дальнейшем:

1. Нахождение такой f (х), удовлетворяющей УФР, чтобы в рабочем интервале , где - заданная точность воспроизведения. Назовём это этапом аппроксимации.

2. Конструирование по найденной f (х) электрической цепи. Назовём это этапом реализации.

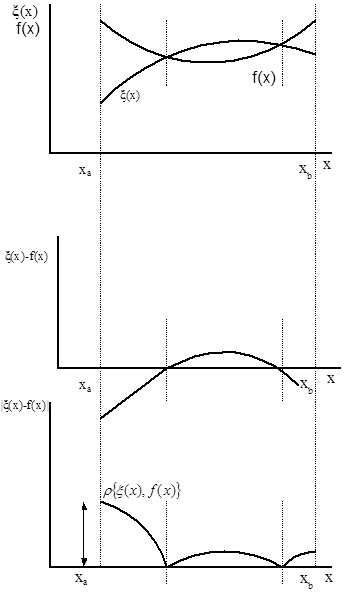
Рисунок 1.

Методы аппроксимации заданных характеристик

В общем случае задача аппроксимации состоит в конструировании функций , удовлетворяющей УФР в заданном элементном базисе и воспроизводящей с требуемой точностью в рабочем интервале заданную графически (либо таблицей, либо аналитически) зависимость ξ(х) , a– варьируемые коэффициенты, значения которых и должны быть найдены в результате решения задачи аппроксимации.

Из-за недостатка времени не представляется возможным осветить все известные методы решения этой задачи. Поэтому остановимся с одной стороны на простейшей из них, имеющих достаточно большую историю их практического применения, а с другой стороны – с современными численными методами, являющимися не только универсальными, но и самыми эффективными при отыскании оптимальных решений с помощью ЭВМ.

а) Интерполирование функций

При интерполировании коэффициенты аппроксимирующей функции выбираются такими, чтобы значения заданной функции ξ(х) совпадали бы в некотором числе заранее выбранных точек х₁ , х₂ ,.....,х_n , называемыми точками или узлами интерполирования.

Ясно, что указанное условие позволяет составить систему из N уравнений с N неизвестными

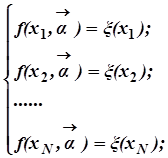
Её решение позволяет определить все варьируемые параметры .

Преимущества метода:

- ξ (х) может быть задана в любой форме;

- простота решения.

Наряду с преимуществами, метод интерполирования обладает двумя существенными недостатками:

- в ходе решения задачи аппроксимации не контролируется точность приближения функций d;

- полученная аппроксимирующая функция f (x) может не удовлетворять УФР. В этом случае выбираются новые узлы интерполирования, хотя и в этом случае нет гарантии выполнения УФР.

б) Аппроксимация по Тейлору.

Этот вид аппроксимации требует задания функции ξ (х) в виде аналитического выражения. При этом функции f (x) и ξ (х) должны допускать разложение в ряд Тейлора в некоторой точке x=х₀ .

Если N – число варьируемых коэффициентов функции f (х), то в точке x=х₀ должны быть равны значения функций f (х) и ξ (х), а также N-1 их производных младших порядков, т.е.

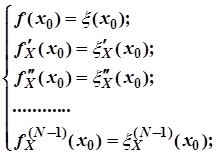
Решив систему уравнений, найдём значения параметров (коэффициенты уравнения f (х)).

Хотя такой аппроксимации присущи как и при интерполировании недостатки, однако на практике она находит широкое применение.