Реферат: Основные теоремы теории электрических цепей

Основные понятия топологии электрических цепей

Теорема замещения

Теорема Теллегена. Баланс мощности

Принцип дуальности

Заключение

Литература

Основные понятия топологии электрических цепей

При анализе конкретной электрической цепи, она представляется в виде совокупности соединенных между собой активных и пассивных элементов. Место соединения зажимов двух и более элементов называется узлом электрической цепи. В отдельных случаях целесообразно различать узлы простые и сложные .

Простым узлом называют место соединения зажимов двух элементов (рис. 1. 1, а), а сложным – место соединения зажимов трех и более элементов (рис. 1. 1, б).

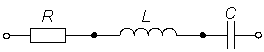
а) простые узлы;

б) узел сложный.

Рис. 1. 1.

Обобщением понятия элемента как соединительного пути между двумя узлами цепи является понятие ветви цепи .

Ветвь – это часть цепи, которая включена между двумя узлами и взаимодействует (обменивается энергией) с остальной цепью только через эти два узла. Таким образом, ветвь – это двухполюсная электрическая цепь – двухполюсник. Графическое изображение совокупности узлов цепи и соединительных путей между ними, т. е. ветвей цепи, называется графом цепи . В качестве примера на рис. 1.2. показаны схема и граф цепи.

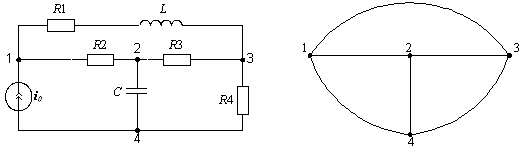
Рис. 1.2.

Последовательность ветвей, соединяющих два узла, определяет топологическое понятие пути . При этом предполагается, что через промежуточные узлы путь проходит один раз.

Под контуром электрической цепи принято понимать любой замкнутый путь на графе, который начинается и кончается в узле. Иными словами, контуром является связный подграф, в котором к каждому узлу присоединены по две ветви. На рис. 1.2 в качестве примера можно привести контуры: 1-2-4-1, 1-2-3-4-1 и др. Число контуров, которые вообще можно выделить в схеме цепи, отличается от числа так называемых независимых контуров. Независимыми будут, в частности, такие контуры, каждый из которых включает хотя бы один элемент (ветвь), не содержащийся в других контурах.

Дерево графа называют систему наименьшего числа ветвей, связывающих все узлы графа без образования контуров. Следовательно, дерево представляет связный подграф, который содержит все узлы графа и получается путем удаления всех ветвей, образующих контуры. Для заданного графа существует множество деревьев. На рис. 1.3. приведены некоторые из деревьев рассмотренного графа.

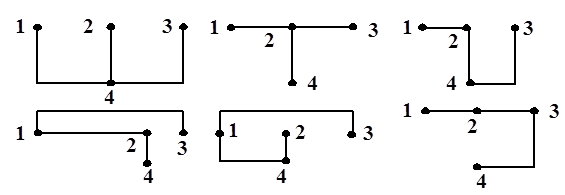
Рис. 1. 3.

Из рисунка видно, что между парой узлов дерева имеется единственный путь. Построение дерева разбивает ветви графа на ветви дерева и ветви, не вошедшие в дерево, называемые ветвями связи или хордами. Число ветвей дерева на единицу меньше числа узлов:

.

Это следует из того, что первая ветвь соединяет два узла, а каждая последующая ветвь присоединяет один узел.

Число ветвей связи (число независимых контуров) равно числу остальных ветвей, не вошедших в дерево:

.

Совокупность ветвей связного графа называется сечением , если, во-первых, устранение всех ветвей этой совокупности (узлы графа сохраняются) делает граф несвязным и, во-вторых, после восстановления любой из ветвей этой совокупности вновь образуется связный граф. На графе (схеме) цепи сечение цепи изображается в виде тонкой или штриховой линии, которая проходит через все ветви сечения. Для графа рис. 1.4.,а одно из возможных сечений содержит ветви, включенные между узлами 1-2, 02, 0-3, 3-4.

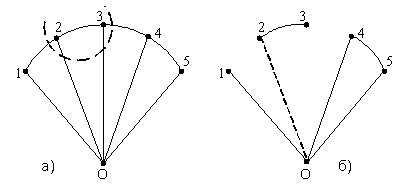
--> ЧИТАТЬ ПОЛНОСТЬЮ <--