Реферат: Основные теоремы теории электрических цепей

После удаления этих ветвей образуется несвязный граф рис. 1.4.,б и, следовательно, выполняется первое из требований определения. Выполняется так же и второе требование, поскольку добавление к графу рис. 1.4.,б любой из ветвей выбранного сечения приводит к связному графу.

Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа.

Теорема замещения

В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения : значения всех напряжений и токов в электрической цепи сохраняются неизменными, если любую ветвь цепи заменить источником напряжения, у которого задающее напряжение равно напряжению этой ветви до указанной замены.

Для доказательства теоремы обратимся к рис. 1.5. а, на котором выделена ветвь цепи, подлежащая замене источником напряжения.

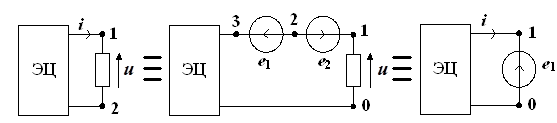
а) б) в)

Рис. 1.5.

Введем последовательно с этой ветвью два источника напряжения с задающими напряжениями и включим их так, как показано на
рис. 1.5.,б. При этом все напряжения и токи сохраняют свои прежние значения, поскольку задающие напряжения источников компенсируют друг друга (разность потенциалов между узлами 1 и 3 цепи равна нулю, что эквивалентно соединению этих узлов накоротко). Но компенсируют друг друга также напряжение на зажимах выделенной ветви и задающее напряжение одного из источников, т. е. напряжение между узлами 0 и 2 цепи. Эти два элемента не влияют, следовательно, на токи и напряжения в цепи, и их можно исключить из цепи, соединив накоротко узлы 0 и 2. Но тогда в цепи вместо выделенной ветви оказывается включенным источник напряжения (рисунок 1.5.,в), что и доказывает теорему.

Аналогично может быть доказана и двойственная (дуальная) формулировка теоремы замещения : значения всех напряжений и токов в электрической цепи сохраняются неизменными, если любую ветвь цепи заменить источником тока, у которого задающий ток равен току в этой ветви до указанной замены.

Доказательство предполагается выполнить самостоятельно.

В качестве примера применения теоремы на рисунке 1.6 приведены схемы трех цепей.

Рис. 1. 6.

В схемах в соответствии с теоремой замещения напряжения и токи в одноименных ветвях имеют одинаковые значения. Необходимо обратить внимание на то, что теорема применима как к линейным, так и к нелинейным электрическим цепям. Так как при ее доказательстве на выделенную ветвь не накладывается никаких ограничений, кроме того, что она обменивается энергией с остальной частью цепи только через зажимы 1-0 с помощью тока.

Теорема Теллегена. Баланс мощности

Теорема Теллегена является одной из наиболее общих теорем теории электрических цепей. Рассмотрим граф произвольной электрической цепи, содержащей n _в ветвей и n _у узлов. Для согласованных направлений напряжений и токов ветвей теорема Теллегена гласит: сумма произведений напряжений u_k и токов i_k всех ветвей графа, удовлетворяющих законам Кирхгофа, равна нулю.

.

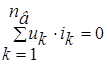Докажем эту теорему на примере цепи, изображенной на рис. 1. 7.

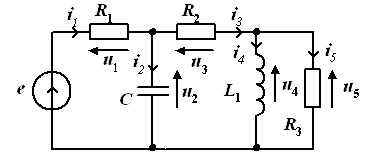
Рис. 1.7.

Составим сумму произведений для каждой из ветвей:

.

Согласно второго закона Кирхгофа должны выполняться условия:

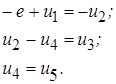
Подставим данные выражения напряжений в сумму:

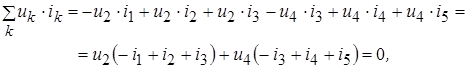
так как выражения, стоящие в скобках, согласно первого закона Кирхгофа равны нулю, это и доказывает теорему. Необходимо подчеркнуть, что поскольку теорема Теллегена следует непосредственно из законов Кирхгофа, то она справедлива для любых электрических цепей: линейных и нелинейных, активных и пассивных; цепей, параметры которых изменяются во времени (параметрических цепей). В общем случае эта теорема справедлива и для случая попарных произведений и разных ветвей, если для них выполняются законы Кирхгофа.

Из теоремы Теллегена вытекает ряд следствий, важнейшим из которых является баланс мощности. Действительно, произведение представляет собой мгновенную мощность k -ветви, поэтому в соответствии с формулой алгебраическая сумма мощностей всех ветвей цепи равняется нулю. Если выделить ветви с независимыми источниками, то баланс мощности можно сформулировать следующим образом: алгебраическая сумма мощностей, отдаваемых независимыми источниками, равняется алгебраической сумме мощностей, потребляемых остальными ветвями электрической цепи .

Пример. Составит баланс мощности для цепи, изображенной на рис. 1.8.