Реферат: Основы графической визуализации вычислений
· возможность построения сечений трехмерных фигур и поверхностей плоскостями;
· функциональная многоцветная и полутоновая окраска;
· возможность имитации световых эффектов при освещении фигур точечным источником света;
· возможность создания анимационной графики;
· возможность создания объектов для типового интерфейса пользователя.
Построение графика функций одной переменной
В режиме непосредственных вычислений доступны практически все возможности системы. Широко используется построение графиков различных функций, дающих наглядное представление об их поведении в широком диапазоне изменения аргумента. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах.
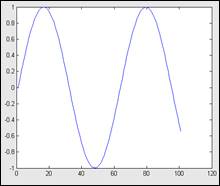
Рассмотрим простейший пример - построение графика синусоиды. MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками. Зададим интервал изменения аргумента xот 0 до 10 с шагом 0.1. Для построения графика достаточно вначале задать вектор х=0:0.1:10, а затем использовать команду построения графиков plot (sin(x)).
Вектор xзадает интервал изменения независимой переменной от 0 до 10 с шагом 0.1. Функция plotстроит не истинный график функции sin(x), а лишь заданное числом элементов вектора xчисло точек. Эти точки затем просто соединяются отрезками прямых, т. е. осуществляется кусочно-линейная интерполяция данных графика. При 100 точках полученная кривая глазом воспринимается как вполне плавная, но при 10 - 20 точках она будет выглядеть состоящей из отрезков прямых.
MATLAB строит графики в отдельных окнах, называемых графическими окнами. В главном меню окна команды пункта меню Tools (Инструменты), позволяют вывести или скрыть инструментальную панель. Средства этой панели позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.
Построение в одном окне графиков нескольких функций
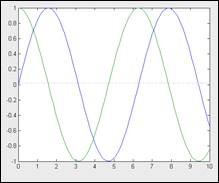
Построим графики сразу трех функций:sin(x), cos(x) и sin(x)/х. Прежде всего, отметим, что эти функции могут быть обозначены переменными, не имеющими явного указания аргумента в виде у (x):
>>y1=sin(x); y2=cos(x); y3=sin(x)/x;
Такая возможность обусловлена тем, что эти переменные являются векторами - как и переменная x. Теперь можно использовать одну из ряда форм команды
plot: plot(a1, f1, a2, f2, a3, f3,...).
где a1, a2, a3,…- векторы аргументов функций, а f1, f2, f3,... - векторы значений функций, графики которых строятся в одном окне. В нашем случае для построения графиков указанных функций мы должны записать следующее:
>> plot (x, y1, x, y2, x, y3)
Можно ожидать, что MATLAB в этом случае построит, как обычно, точки графиков этих функций и соединит их отрезками линий. Но, если мы выполним эти команды, то никакого графика не получим вообще. Не исключен даже сбой в работе программы. Причина этого казуса возникнет при вычислении функции y3=sin(x)/x, если x представляет собой массив (вектор), то нельзя использовать оператор матричного деления /.
Чтобы получить график, надо вычислять отношение sin(x) к x с помощью оператора поэлементного деления массивов ./ .
>>y1=sin(x); y2=cos(x); y3=sin(x)./x;
Warning: Divide by zero.
(Type "warning off MATLAB:divideByZero" to suppress this warning.)
>> plot(x,y1,x,y2,x,y3)
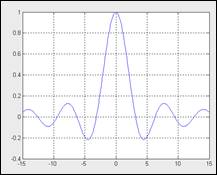
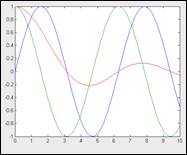
MATLAB построил графики всех трех функций, но в окне командного режима появилось предупреждение о делении на 0 - в момент, когда х=0. Это говорит о том, что plot «не знает» о том, что неопределенность sin(x)/x=0/0 устранима и дает 1. Это недостаток практически всех систем для численных вычислений.
Графическая функция fplot