Реферат: Основы расчета надежности технических систем по надежности их элементов

Т₀ = 2ехр(-5lt)-5ехр(-4lt)+2ехр(-3lt)+2ехр(-2lt)dt=
= (49/60)´(1/l). (4.5.20)

Пример 4.5.9. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.3,б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9.

Решение.

Так как все элементы идентичны, воспользуемся формулой (4.5.18); с ее помощью получаем:

Р = 2´0,9⁵ - 5´0,9⁴ +2´0,9³ + 2´0,9² »0,978.

Пример 4.5.10. Требуется определить вероятность безотказной работы и среднюю наработку на отказ системы, состоящей из пяти независимых и одинаковых элементов, соединенных по мостиковой схеме (рис. 4.5.3,б); считается, что l=0,0005ч^-1 , t=100ч и все элементы начинают работать в момент времени t=0.

Решение.

1. С помощью формулы (4.5.19) получаем
Р₍₁₀₀₎ = 2е^-0,25 -5е^-0,2 +2е^-0,15 +2е^-0,1 = 0,9999.
2. Подставляя полученное значение вероятности безотказной работы в формулу (4.5.20), находим среднюю наработку на отказ
Т₀ = 49/(60´0,0005) = 1633,4 ч.

Надежность резервированной системы

Одним из путей повышения надежности системы является введение в нее резервных (дублирующих) элементов. Резервные элементы включаются в систему как бы "параллельно" тем, надежность которых недостаточна.

Параллельное соединение резервного оборудования системы

Рассмотрим самый простой пример резервированной системы - параллельное соединение резервного оборудования системы. В этой схеме все n одинаковых образцов оборудования работают одновременно, и каждый образец оборудования имеет одинаковую интенсивность отказов. Такая картина наблюдается, например, если все образцы оборудования держатся под рабочим напряжением (так называемый "горячий резерв"), а для исправной работы системы должен быть исправен хотя бы один из n образцов оборудования.

В этом варианте резервирования применимо правило определения надежности параллельно соединенных независимых элементов. В нашем случае, когда надежности всех элементов одинаковы, надежность блока определяется по формуле (4.5.9)

Р = 1 - (1-р)ⁿ .
Если система состоит из n образцов резервного оборудования с различными интенсивностями отказов, то
P(t) = 1-(1-p₁ ) (1-p₂ )... (1-p_n ). (4.5.21)

Выражение (4.5.21) представляется как биноминальное распределение. Поэтому ясно, что когда для работы системы требуется по меньшей мере k исправных из n образцов оборудования, то
P(t) = 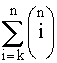pⁱ (1-p)^n-i , где 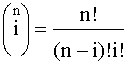. (4.5.22)

При постоянной интенсивности отказов l элементов это выражение принимает вид

P(t) = 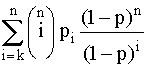, (4.5.22.1)

где р = еxp(-lt).

Включение резервного оборудования системы замещением

В данной схеме включения n одинаковых образцов оборудования только один находится все время в работе (рис. 4.5.11). Когда работающий образец выходит из строя, его непременно отключают, и в работу вступает один из (n -1) резервных (запасных) элементов. Этот процесс продолжается до тех пор, пока все (n -1) резервных образцов не будут исчерпаны.

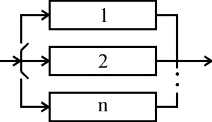
Рис. 4.5.11. Блок-схема системы включения резервного оборудования системы замещением
Примем для этой системы следующие допущения:
1. Отказ системы происходит, если откажут все n элементов.
2. Вероятность отказа каждого образца оборудования не зависит от состояния остальных (n -1) образцов (отказы статистически независимы).
3. Отказывать может только оборудование, находящееся в работе, и условная вероятность отказа в интервале t, t+dt равна ldt; запасное оборудование не может выходить из строя до того, как оно будет включено в работу.
4. Переключающие устройства считаются абсолютно надежными.
5. Все элементы идентичны. Резервные элементы имеют характеристики как новые.

Система способна выполнять требуемые от нее функции, если исправен по крайней мере один из n образцов оборудования. Таким образом, в этом случае надежность равна просто сумме вероятностей состояний системы, исключая состояние отказа, т.е.
Р(t) = еxp(-lt) 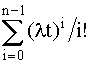. (4.5.23)

В качестве примера рассмотрим систему, состоящую из двух резервных образцов оборудования, включаемых замещением. Для того чтобы эта система работала, в момент времени t, нужно, чтобы к моменту t были исправны либо оба образца, либо один из двух. Поэтому
Р(t) = еxp(-lt) 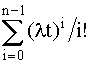=(exp(-lt))(1+ lt). (4.5.24)

На рис. 4.5.12 показан график функции Р(t) и для сравнения приведен аналогичный график для нерезервированной системы.

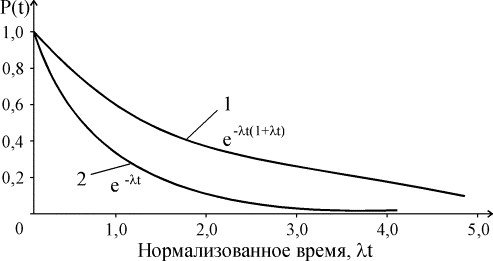Рис. 4.5.12. Функции надежности для дублированной системы с включением резерва замещением (1) и нерезервированной системы (2)

Пример 4.5.11. Система состоит из двух идентичных устройств, одно из которых функционирует, а другое находится в режиме ненагруженного резерва. Интенсивности отказов обоих устройств постоянны. Кроме того, предполагается, что в начале работы резервное устройство имеет такие же характеристики, как и новое. Требуется вычислить вероятность безотказной работы системы в течение 100 ч при условии, что интенсивности отказов устройств l=0,001 ч^-1 .

Решение. С помощью формулы (4.5.23) получаем Р(t) = (exp(-lt))(1+ lt).

При заданных значениях t и l вероятность безотказной работы системы составляет

Р(t) = е^-0,1 (1+0,1) = 0,9953.

Во многих случаях нельзя предполагать, что запасное оборудование не выходит из строя, пока его не включат в работу. Пусть l₁ - интенсивность отказов работающих образцов, а l₂ - резервных или запасных (l₂ >0). В случае дублированной системы функция надежности имеет вид:
Р(t) = ехр(-(l₁ +l₂ )t) + 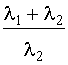ехр(-l₁ t) - 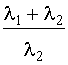ехр(-(l₁ +l₂ )t).

Данный результат для k=2 можно распространить на случай k=n. Действительно

Р(t) = ехр(-l₁ (1+a(n-1))t) 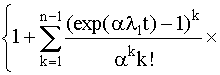(4.5.25)
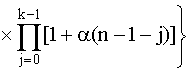, где a = l₂ /l₁ > 0.

Надежность резервированной системы в случае комбинаций отказов и внешних воздействий

В некоторых случаях отказ системы возникает вследствие определенных комбинаций отказов образцов входящих в систему оборудования и (или) из-за внешних воздействий на эту систему. Рассмотрим, например, метеоспутник с двумя передатчиками информации, один из которых является резервным или запасным. Отказ системы (потеря связи со спутником) возникает при выходе из строя двух передатчиков или в тех случаях, когда солнечная активность создает непрерывные помехи радиосвязи. Если интенсивность отказов работающего передатчика равна l, а j - ожидаемая интенсивность появления радиопомех, то функция надежности системы
Р(t) = еxp(-(l+j)t) + l t еxp(-(l+j)t). (4.5.26)

Данный тип модели также применим в случаях, когда резерв по схеме замещения отсутствует. Например, предположим, что нефтепровод подвергается гидравлическим ударам, причем воздействие незначительными гидроударами происходит с интенсивностью l, а значительными - с интенсивнностью j. Для разрыва сварных швов (из-за накопления повреждений) трубопроводу следует получить n малых гидроударов или один значительный.

Здесь состояние процесса разрушения представляется числом ударов (или повреждений), причем один мощный гидроудар равносилен n малых. Надежность или вероятность того, что трубопровод не будет разрушен действием микроударов к моменту времени t равна: