Реферат: Оценка стоимости ценных бумаг

N _обл – номинальная стоимость (номинал) облигации.

Принимая требуемую инвестором ставку доходности постоянной из года в год, уравнение (3) можно упростить:

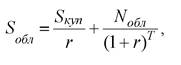
Например, инвестор приобрел облигацию номиналом 1000 руб. с купонной ставкой 10%, которая соответствует ежегодной выплате 100 руб. Предположим, что требуемая в данный момент инвестором ставка доходности для этого типа облигаций составляет 20%, а срок до погашения - 3 года. Приведенная стоимость такой ценной бумаги будет рав­няться:

S _обл = 100/1,2 + 100/1,2² + 100/1,2³ + 1000/1,2³ ≈ 789,35 руб.

При больших значениях параметра T для вычисления по этой формуле целесооб­разно пользоваться таблицами аннуитета (в данном случае находится аннуитет при 20% в течение 3-х периодов).

Так как действительная стоимость облигации S _обл в данном случае меньше номи­нальной N_обл , то при нормальной рыночной ситуации такая облигация должна продаваться с дисконтом относительно номинала. Это является следствием того, что требуемая ставка доходности оказалась больше, чем купонная ставка облигации.

Если действительная стоимость облигации меньше номинальной, то при нормальной рыночной ситуации такая облигация должна прода­ваться с дисконтом относительно номинала. Если действительная стоимость – больше номинала, облигация должна продаваться с пре­мией.

Предположим теперь, что вместо ставки дисконтирования 20% для некоторой об­лигации используется ставка 8% (т. е. новая облигация характеризуется значительно меньшим риском, чем прежняя). Значение приведенной стоимости в данном случае будет иным:

S _обл = 100/1,08 + 100/1,08² + 100/1,08³ + 1000/1,08³ ≈ 1051,54 руб.

В этом случае действительная стоимость новой облигации S_обл превышает ее номи­нальную стоимость N_обл , равную 1000 руб., поскольку требуемая ставка доходности ока­зывается меньше купонной ставки этой облигации. Чтобы купить эту облигацию, в нор­мальной рыночной ситуации инвесторы готовы платить премию (надбавку к номинальной стоимости).

Если требуемая ставка доходности равняется купонной ставке облигации (что слу­чается довольно редко и, как правило, в момент первичного размещения облигаций), при­веденная стоимость облигации обычно равняется ее номинальной стоимости.

2.3.2. Бескупонные облигации

Согласно Федеральному закону РФ «Об акционерных обществах» от 26 декабря 1995 г. № 208-ФЗ, облигация удостоверяет право ее владельца требовать погашения обли­гации (выплату номинальной стоимости или номинальной стоимости и процентов) в уста­новленные сроки. Таким образом, выплата купонных процентов – не является обязатель­ным условием эмиссии облигаций.

Бескупонная облигация не предусматривает периодических выплат процентов, зато продается со значительным дисконтом относительно своего номинала. Покупатель такой облигации получает доход, который образуется за счет постепенного увеличения действи­тельной стоимости S_обл относительно ее первоначальной покупной цены (цены ниже ее номинальной стоимости), пока облигация не будет выкуплена по своей номинальной стоимости в день ее погашения.

7

Бескупонная облигация не предусматривает периодических выплат процентов. Ее владелец получает доход за счет дисконта (скидки) на цену облигации.

Уравнение определения действительной стоимости бескупонной облигации пред­ставляет собой усеченный вариант уравнения (4), применяемого для обычной облигации (т. е. облигации, по которой выплачиваются проценты). Компонент «приведенная стои­мость процентных платежей» исключается из уравнения, и приведенная стоимость обли­гации оценивается лишь «приведенной стоимостью основного платежа в момент погаше­ния облигации»:

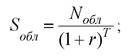(5)

2.3.3. Облигации с полугодовыми и ежеквартальными купонами

На современном российском рынке представлены, главным образом, облигации с ежегодными выплатами. Однако, например, в США принято использовать полугодовые выплаты (даже облигации с ежегодными выплатами при сравнении их доходности приво­дятся к виду, соответствующему аналогичным инструментам с полугодовыми выплата­ми). В ряде случаев в мировой практике используются также облигации с ежеквартальны-

Если проценты на облигацию начисляются раз в полгода, уравнение (3) модифици­руется к виду:

(6)

где:

r – по-прежнему номинальная требуемая годовая процентная ставка;

S _куп /2 – полугодичные купонные выплаты по облигации;

2n – общее количество полугодичных купонных выплат до наступления срока по­гашения облигации.

Аналогично уравнение (3) можно модифицировать для случая начисления процен­тов раз в квартал:

(7)

При начислении купонного дохода раз в полугодие или раз в квартал соответст­вующие модификации претерпит и уравнение действительной стоимости (1) для бессроч­ных облигаций: