Реферат: Параметри тунельного ефекту

1. Тунельний ефект

Розглянемо поведінку частки при проходженні через потенційний бар'єр. Нехай частка, що рухається ліворуч праворуч, зустрічає на своєму шляху потенційний бар'єр висоти U₀ і ширини l (мал. 1.1). По класичних виставах рух частки буде таким:

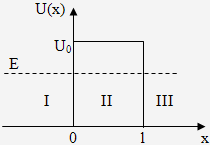
Мал.1.1 Проходження частки через потенційний бар'єр

- якщо енергія частки буде більше висоти бар'єра (E>U₀ ), то частка безперешкодно проходить над бар'єром;

- якщо ж енергія частки буде менше висоти бар'єра (E<U₀ ), то частка відбивається й летить у зворотну сторону;

- крізь бар'єр частка проникнути не може.

Зовсім інакше поведінка частки за законами квантової механіки.

По-перше, навіть при E>U₀ є відмінна від нуля ймовірність того, що частка відіб'ється від потенційного бар'єра й полетить назад. По-друге, при E<U₀ є імовірність того, що частка проникне « крізь» бар'єр і розміститься в області III. Така поведінка частки описується рівнянням Шредінгера:

. (1.1)

Тут- хвильова функція мікрочастинки. Рівняння Шредінгера для області I і III буде однаковим. Тому обмежимося розглядом областей I і II. Отже, рівняння Шредінгера для області I прийме вид:

, (1.2)

увівши позначення:

, (1.4)

остаточно одержимо:

(1.5).

Аналогічно для області II:

, (1.6)

де. Таким чином, ми одержали характеристичні рівняння, загальні рішення яких мають вигляд:

приx<0,(1.7)

приx>0(1.8)

Доданок відповідає хвилі, що поширюється в області I у напрямку осі х, А_1- амплітудацієї хвилі. Доданоквідповідає хвилі, що поширюється в області I у напрямку, протилежному х. Це хвиля, відбита від бар'єра, В_1- амплітуда цієї хвилі. Тому що ймовірність знаходження мікрочастинки в тому або іншому місці простору пропорційна квадратуамплітуди хвилі де Бройля, те відношення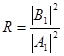являє собою коефіцієнт відбиття мікрочастинки від бар'єра.

Доданок відповідає хвилі, що поширюється в області II у напрямку х. Квадрат амплітуди цієї хвилі відбиває ймовірність проникнення мікрочастинки в область II. Відношення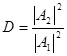являє собою коефіцієнт прозорості бар'єра.

Доданокповинний відповідати відбитій хвилі, що поширюється в області II. Тому що такої хвилі ні, те В₂ слід покласти рівним нулю.

Для бар'єра, висота якого U>E, хвильовий вектор k₂ є уявним. Покладемо його рівним ik, деє дійсним числом. Тоді хвильові функціїй придбають наступний вид:

(1.9)

(1.10)

Тому що, те це значить, що є ймовірність проникнення мікрочастинки на деяку глибинув другу область. Ця ймовірність пропорційна квадрату модуля хвильовоїфункції:

. (1.11)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--