Реферат: Переключательные функции одного и двух аргументов

Используя соотношение , получаем

f₅₈ (x₁ ,x₂ ,x₃ )=(1 Å x₁ )x₂ (1 Å x₃ ) Å (1 Å x₁ )x₂ x₃ Å x₁ (1 Å x₂ )(1 Å x₃ ) Å x₁ x₂ (1 Å x₃ ).

Приводя подобные члены, окончательно находим

f ₅₈ ( x ₁ , x ₂ , x ₃ )= x ₁ Å x ₂ Å x ₁ x ₂ Å x ₁ x ₃ .

3. Совершенная дизъюнктивная нормальная форма переключательной функции.

В общем виде пере­ключательная функция п аргументов может быть задана таблицей истинности. Обозначим через f_{( i )} (i=0, … ,2ⁿ -1) значение функции на i-м наборе аргументов. Напомним, что каждая из величин f_{( i )} принимает значение нуль или единица. В соот­ветствие i-му набору аргументов можно поставить конституенту единицы Ki , которая принимает значение, равное единице только на данном f _{( i )} наборе. Умножим каждую конституенту единицы Ki на значение функ­ции f_{( i )} и рассмотрим дизъюнкцию произведений f_i K_i :

. (3)

Если подставить в выражение (3) значения f_(i) , то получим дизъюнкцию конституент, которые равны еди­нице на тех же наборах, что и заданная функция. Дей­ствительно, ввиду того, что 0×x =0 и 0Úх=х, члены вы­ражения (2), в которых коэффициенты f _{( i )} =0, можно опустить, а так как x × 1 = x , то коэффициенты f _{( i )} = 1можно не писать. Тогда

где j₁ , …,j_m – номера наборов, на которых функция равна единице;

m – число таких наборов.

Определение 3. Дизъюнкция конституент единицы, равных единице на тех же наборах, что и заданная функция, называется совершенной дизъюнктивной нормальной формой переключательной функции.

Любую переключательную функцию f ( x ₁ , . . . , x_n ) (кроме константы ноль) можно представить в совершенной дизъюнктивной нормальной форме. Заметим, что любая переключательная функция имеет единственную совершенную дизъюнктивную нормальную форм у: это непосредственно следует из выражения (3).

Совершенную дизъюнктивную нормаль­ную форму переключательной функции удобно находить в такой последователь­ности:

· выписать ряд произведений всех аргументов и соединить их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в единицу;

· записать под каждым произведением набор аргу­ментов, на котором функция равна единице, и над аргу­ментами, равными нулю, поставить знаки отрицания.

Это правило называют иногда правилом запи­си переключательной функции по единицам.

Пример 4. Представить в совершенной дизъюнктивной нормальной форме переключательную функцию четырех аргументов f ₂₃₈₀₅ ( x ₁ , x ₂ , x ₃ , x ₄ ) (см. табл. 2).

Решение. Из табл. 2 видно, что переключательная функция принимает значения, равные единице, на следующих наборах аргументов:

0001, 0011, 0100, 0101, 1000, 1001, 1010, 1011, 1100, 1101, 1111.

Таким образом, совершенная дизъюнктивная нормальная форма функции f ₂₃₈₀₅ ( x ₁ , x ₂ , x ₃ , x ₄ ) будет состоять из одиннадцати дизъюнкций, каждая из которых представляет собой конъюнкцию четырех элементов:

4. Совершенная конъюнктивная нормальная форма переключательной функции.

Если заданная переключательная функция равна единице на большинстве наборов аргументов, то представление функции в совершенной дизъюнктивной нормальной форме может оказаться достаточно громоздким. В этих случаях удобнее использовать другую форму представления функции – совершенную конъюнктивную нормальную форму. Для представления функций в этой форме используется функция конституенты нуля.

Рассмотрим выражение

, (4)

где f _{( i )} – значение переключательной функции на i -м наборе.

Ввиду справедливости соотношений 1Úx = 1 и 0 Ú х= х, при подстановке в выражение (4) значений функ­ции f_(i) , сомножители, у которых f_(i) , == 1, можно опустить, а значения функции f_(i) =0 не писать. Тогда

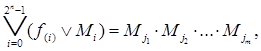(5)