Реферат: Перспективные аспекты развития физико-топологических представлений о времени

Определившись по некоторым общим ключевым вопросам топологической интерпритации конструкции Времени [3], перейдем к анализу двух частных положений, которые тесным образом связаны с топологическим Временем.

Поскольку, с одной стороны, при задании топологического Времени мы руководствовались строгими принципами топологии, как одной из основных математических структур, а с другой стороны - оперируя реальной спецификой хронологической изменчивости в сложных и масштабных системах, то в связи с этим необходимо выяснить физическую сущность таких составных частей Временной топологии, как пустое множество и множество Настоящего PR .

Запишем следующие две формулировки.

Первая: показать условность существования на универсальном множестве Времени пустого множества и физически обосновать элиминировку этой категории на.

Вторая: представить аргументы в пользу существования переменного характера у Настоящего, которое выражается в том, что при общих физических оценках PR не входит в в явном виде.

Наиболее полное на наш взгляд, решение поставленных выше частных задач можно получить в том случае, если к ним применить алгоритмы алгебры Буля (G. Boole) [5], т.е. алгебры производящей теоретико-множественные операции над множествами. Эта алгебра имеет своеобразные законы действия, которые существенно отличаются от законов действия над числами.

Сформулируем такое предложение.

Предложение 1.

В физически реалистических условиях на универсальном множестве Времени не просматриваются области индетифицирующиеся с пустым множеством .

Дано:.Доказать:.

Доказательство:

1) Перепишем общее выражение для универсального множества Времени

( 2 )

2) В теории множеств всякое пустое множество можно представить, как пересечение некоторого множества и его дополнения. Под дополнением множества в алгебре Буля понимается множество всех элементов универсального множества не принадлежащих исходному множеству. Таким образом, легко записать тремя способами

(3)

Вообще - то, запись пустого множества в виде триплета ( 3 ) не лишена целесообразности, поскольку мы должны, в силу существования топологии Времени, учитывать все три спектральных компаненты Времени и их дополнения.

3) Учитывая ( 3 ) перепишем ( 2 ) в виде

, (4.1)

, (4.2 )

, ( 4.3)

Здесь, весьма важным являтся тот факт, что в булевой алгебре при правилах действия над множествами, сведенных в равенства, необходимо строго соблюдать чередование, слева и справа, членов в этих выражениях.

4) Проанализируем формулу ( 4.1 )

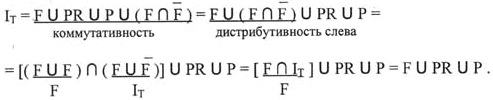
Что и требовалось доказать, т.е..

5) Рассмотрим равенство (4.2 )

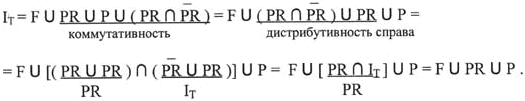
Доказали существование равенства вида

6) И, в заключении, проверим выражение (4.3 )