Реферат: Первая краевая задача для уравнения теплопроводности в нецилиндрической неограниченной области
,
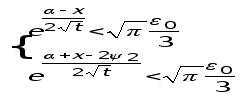откуда:
. (8)
Т. к. в работе исследуется поведение неравенства (3) при 
то принимаем что для некоторого 
:
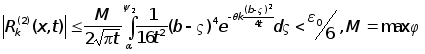. (9)
3. Формулировка результата в виде теоремы
Обобщая результаты всей работы в целом можно сформулировать следующие теоремы:
1. Пусть для уравнения теплопроводности имеет место задача
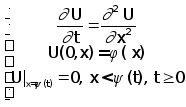(З)
- гладкая, непрерывно - дифференцируемая функция на 
,а функция 
ограничена на R : 
.
Тогда для любого сколь малого числа 
можно указать число
,
такое что имеет место следующая оценка «сверху» решения задачи (З):
Раскрыв квадратные скобки, получим:
.
-
Пусть в имеет место задача (З),
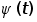- монотонная, неограниченная, возрастающая функция, 
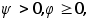тогда: -
если
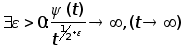, то
2) если 
то
Замечанние:видно, что оценку полученную в теореме 2 можно получить и при более слабых ограничениях 
4. Примеры
Пусть 
, 
-
-
.
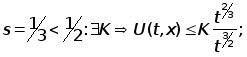
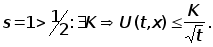Заключение
В дипломной работе произведена оценка решения «сверху» для уравнения теплопроводности с движущей границей по заданному закону. Аналогично, можно получить оценку решения «снизу». Для этого нужно рассмотреть ступенчатую область, в которой для каждой ступеньки решение может быть получено согласно 2.1 (2) . Число таких ступенчатых областей необходимо выбрать таким образом, чтобы оценка полученная снизу была сравнима с полученной выше оценкой.
СПИСОК ЛИТЕРАТУРЫ
-
А. Н. Тихонов, А. А. Самарский, Уравнения математической физики. Изд. «Наука», М. 1966 (с. 230 -233);
-
С. К. Годунов, Уравнения математической физики. Изд. «Наука», М. 1973 . 33-34);
-
Л. Д. Кудрявцев, Краткий курс математического анализа. Изд. «Наука», М. 1989.