Реферат: Первая краевая задача для уравнения теплопроводности в нецилиндрической неограниченной области

Введение

В ряде случаев оказывается невозможным или неприемлемым получение аналитического решения поставленной задачи. Использование основных теорем и положений анализа позволяет получить качественную картину поведения функции решения в заданной области, оценить скорость сходимости решения. Такой подход широко реализуется в областях техники, где получение результата необходимо с заданной точностью.

1.Постановка задачи

В дипломной работе рассматривается задача:

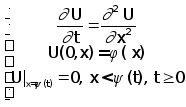(З)

0.

t

x

Требуется привести пример оценки решения задачи (З) в области , и исследовать полученную оценку при

2. Оценочный анализ решения задачи.

Оценка решения задачи (З) основывается на принципе максимума для уравнения теплопроводности : «Всякое решение уравнения в прямоугольнике , непрерывное вплоть до границы, принимает свои наибольшее и наименьшее значения на нижних или на боковых его границах» [2].

2.1. Оценка решения сверху.

В области t=t , x= рассмотрим решение задачи :

, V(0,x) = ( x ), x , (1)

это решение имеет вид [1]:

v (t, x) = . (2)

Зафиксируем некоторое и перейдем к исходной системе координат, тогда (2) в системе t=t, x= будет выглядеть так:

V(t, x) = (2’)

Из принципа максимума [2] заключаем, что:

U( t, x ) V( t, x ). (3)

Таким образом задача сводится к оценке интеграла (2).

2.2. Оценка решения в виде интеграла

--> ЧИТАТЬ ПОЛНОСТЬЮ <--