Реферат: Поиск клик в графах
Фактором графа G(X,U) называется частичный граф G(X,U) , в котором каждая вершина обладает полустепенями исхода и захода, равными единице, имеются одна заходящая и одна исходящая дуги.
Базисным графом называется ориентированный частичный граф, образованный из исходного удалением петель и замыкающих дуг.
Связность графа
В общем случае граф может быть представлен несколькими отдельными графами, не имеющими общих дуг. Тогда граф G(X,U) называется несвязным, а каждый из составляющих его графов G1 , G2 ,...Gn - компонентами связности. Граф называется связным, когда каждую его вершину можно соединить с любой другой его вершиной некоторой цепью.
Операции над графами
1. Объединение графов
G3 (X3 ,Гх3 ) = G1 (X1 ,Г1х1 ) È G2 (X2 ,Г2х2 ) , где X3 =X1 È X2 , а Гx3 =Г1x1 È Г2x2
Пример (Рис 1.1).
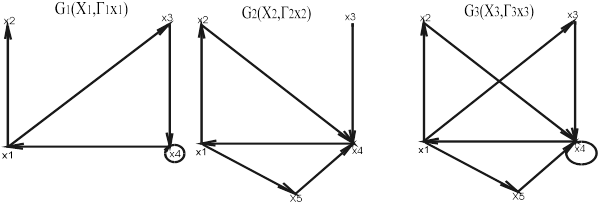 Рис 1.1
Рис 1.1
2. Пересечение графов
G3 (X3 ,Гх3 ) = G1 (X1 ,Г1х1 ) ÇG2 (X2 ,Г2х2 ) , где X3 =X1 Ç X2 , а Гx 3 =Г1x1 Ç Г2x2
Пример (рис 1.2).
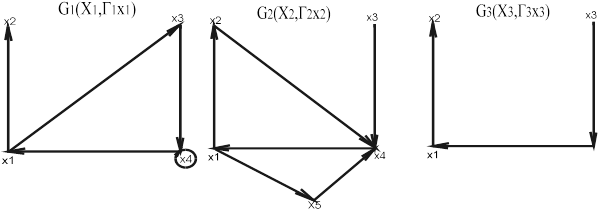 Рис 1.2
Рис 1.2
4. Прямое (декартово) произведение графов.
Прямым произведением множеств Х{x1 .......xn } и Y называется множество Z, элементами которого являются всевозможные пары вида xi , yj , где xi ÎX, yj ÎY. Обозначают: Z=X x Y.
G3 (X3 ,Гх3 ) = G1 (X1 ,Г1х1 ) ÇG2 (X2 ,Г2х2 ) , где X3 =X1 Ç X2, а Гx3 =Г1х1 Ç Г2х2
Пример. (рис 2.3)
G1 (X,Гх)=G1 (X1 ,Гх1 ) G2 (Y,Гy)= G2 (X2 ,Гх2 )
X={x1 x2 x3 } Y={y1 y2 }
Гх1 =0 Гу1 ={y1 y1 }
Гх2 ={x1 x3 } Гу2 ={y1 }
Гх3 =0
Z=X x Y={x 1 y1 , x1 y2 , x2 y1 , x2 y2 , x3 y1 , x3 y2 }
Z={z1 z2 z3 z4 z5 z6 }
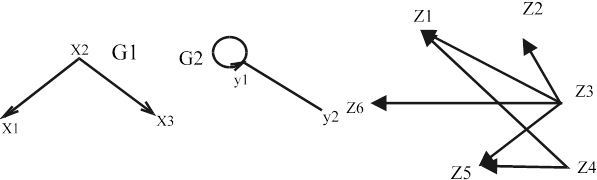
Рис 2.3
7. Расширение графа.
Расширение графа - это превращение, линии, соединяющей любые две вершины графа в элементарный путь введением новых промежуточных вершин на этой линии.
8. Сжатие графа.
Сжатие графа - это превращение элементарного пути, соединяющего две любые вершины графа, в линию.
9. Стягивание графа.